Hand Pose Estimation(1)

最近参加夏令营，到了新的实验室，开始研究新的方向，在已有的两个项目中暂时选择了手势识别相关的方向研究(总觉得这个方向和我之前的方向很像，，)，所以最近开始要看看手势识别相关的论文了，正好最近又打算开始写博客了，刚好就开始在这里记录研究过程了，还是要脚踏实地一步步的往前走啊！

今天看的论文的名字是《3D Hand Shape and Pose Estimation from a Single RGB Image》，是2019年的CVPR的论文。

研究背景

现有的基于RGB信息的3D的手势识别的方法，都只是预测出手的关键点的3D坐标信息，但是还没有方法，从RGB信息中同时估计出手的完整的表面形状以及手的姿势，而这篇论文就是解决了这样一个具有挑战性的问题。

难点与挑战

本文提出，这个问题现在有两大挑战：

1. 首先，与稀疏的3D坐标相比(一个手有21个骨骼关节点要预测)，本文的预测目标要复杂的多(一个手的mesh图中，有1280个未知顶点要预测(dense的很))，现有的解决方法主要是像身体姿态预测里面的那样，将原模型回归成一个预定义的低维参数的可变形的模型，如MANO那样。
2. 目前还缺少真实场景下的3D hand mesh的训练数据集，而人工的给真实场景的RGB图片标记hand mesh真值，相当的麻烦。

贡献

1. 提出了一个基于Graph CNN的端到端的生成hand mesh的可训练网络，可以很好的表示手的变化过程以及捕捉到局部细节。
2. 提出了一个基于真实数据集的弱监督策略来将预训练的网络进行微调，即直接将网络生成的3D mesh渲染成一个depth map，无需在真实数据集上标记就能利用真实场景数据进行训练。
3. 合成了一个大型的基于RGB的数据集，里面有3D hand mesh及hand pose的真值。

Proposed MethodのDetails

提出的网络图如下：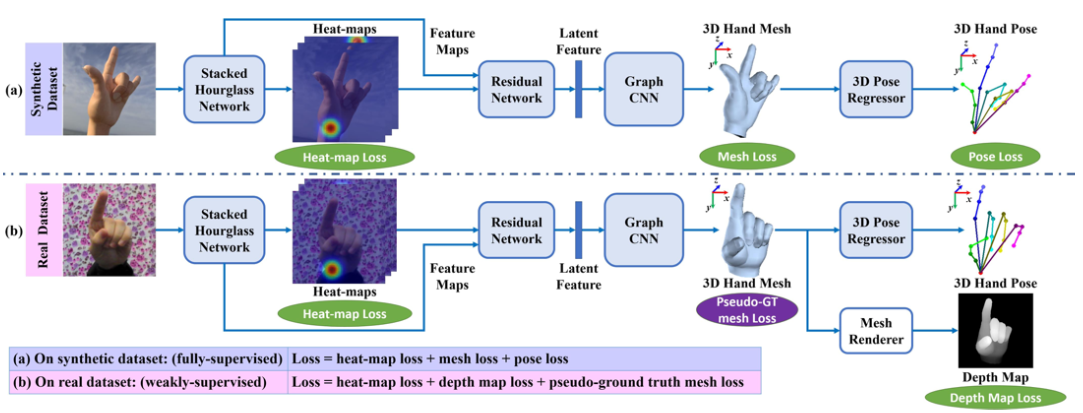

总的来说，网络首先在合成的数据集上训练(heat-map loss, 3D mesh loss, and 3D pose loss)，之后再将网络放在真实数据集上进行弱监督微调，将生成的mesh渲染成depth map进行监督

和MANO的模型变形转换不同，本文将mesh看成一种间接的graph，表示为$
\mathcal{M}=(\mathcal{V}, \mathcal{E}, W)$，其中$\mathcal{V}=\left\{\boldsymbol{v}_{i}\right\}_{i=1}^{N}$表示了mesh的${N}$个顶点，$\mathcal{E}=\left\{\boldsymbol{e}_{i}\right\}_{i=1}^{E}$表示了mesh的${E}$个边，$W=\left(w_{i j}\right)_{N \times N}$则是mesh的邻接矩阵，那么正则化的graph拉普拉斯算子可为$L=I_{N}-D^{-1 / 2} W D^{-1 / 2}$，其中$D=\operatorname{diag}\left(\sum_{j} w_{i j}\right)$为对角的度数矩阵，$I_{N}$为单位矩阵，在本文训练过程中，假设mesh的拓扑不变，即，邻接矩阵$W$不变，以及graph $\mathcal{M}$的拉普拉斯算子$L$不变，$\mathbf{f}=\left(f_{1}, \cdots, f_{N}\right)^{T} \in \mathbb{R}^{N \times F}$为特征，每一个$f$代表了一个顶点的$F$-dim的特征。

网络首先从backbone network中生成需要的feature，再通过以下网络：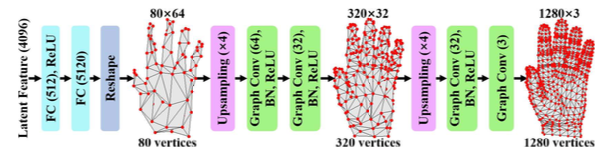

这是一个分层次的结构，不断在graph上执行图卷积操作，让graph由coarse到fine渐渐优化，，，

Loss学习

由于第一次接触Hand Pose Estimation，和之前的显著性物体检测不太一样，之前的loss比较简单，而这个领域的loss感觉比较复杂，刚好这篇论文的loss也挺多的，就正好一起分析一下。

Fully-supervised Training on Synthetic Dataset

Heat-map Loss：$\mathcal{L}_{\mathcal{H}}=\sum_{j=1}^{J}\left\|\mathcal{H}_{j}-\hat{\mathcal{H}}_{j}\right\|_{2}^{2}$
其中$\mathcal{H}_{j}$为真值，$\hat{\mathcal{H}}_{j}$为估计的热力图，其中估计的热力图为64×64 px，而热力图的真值是在以真值的关节点的周围偏离4 px的区域上进行2D高斯操作得到的。

Mesh Loss：$\mathcal{L}_{\mathcal{M}}=\lambda_{v} \mathcal{L}_{v}+\lambda_{n} \mathcal{L}_{n}+\lambda_{e} \mathcal{L}_{e}+\lambda_{l} \mathcal{L}_{l}$
由方程可以发现Mesh Loss由四部分组成，vertex loss $\mathcal{L}_{v}$, normal loss $\mathcal{L}_{n}$, edge loss $\mathcal{L}_{e}$, and Laplacian loss $\mathcal{L}_{l}$，并且$\lambda_{v}=1, \lambda_{n}=1, \lambda_{e}=1, \lambda_{l}=50$。

其中vertex loss是：

$$\mathcal{L}_{v}=\sum_{i=1}^{N}\left\|v_{i}^{3 D}-\hat{v}_{i}^{3 D}\right\|_{2}^{2}+\left\|\boldsymbol{v}_{i}^{2 D}-\hat{v}_{i}^{2 D}\right\|_{2}^{2}$$

${v}_{i}$是指3D或2D的坐标。

其中normal loss是：

$$\mathcal{L}_{n}=\sum_{t} \sum_{(i, j) \in t}\left\|\left\langle\hat{v}_{i}^{3 D}-\hat{v}_{j}^{3 D}, \boldsymbol{n}_{t}\right\rangle\right\|_{2}^{2}$$

用于保证表面法向量的一致性。

其中edge loss是：

$$\mathcal{L}_{e}=\sum_{i=1}^{E}\left(\left\|e_{i}\right\|_{2}^{2}-\left\|\hat{e}_{i}\right\|_{2}^{2}\right)^{2}$$

用于保证边长度的一致性。

其中Laplacian loss是：

$$\mathcal{L}_{l}=\sum_{i=1}^{N}\left\|\boldsymbol{\delta}_{i}-\sum_{\boldsymbol{v}_{k} \in \mathcal{N}\left(\boldsymbol{v}_{i}\right)} \boldsymbol{\delta}_{k} / B_{i}\right\|_{2}^{2}$$

用于保证局部表面的平滑度。

3D Pose Loss：$\mathcal{L}_{\mathcal{J}}=\sum_{j=1}^{J}\left\|\phi_{j}^{3 D}-\hat{\phi}_{j}^{3 D}\right\|_{2}^{2}$

先用heat map loss和3D pose loss分别训练stacked hourglass网络和3D pose regressor，最后再用$\mathcal{L}_{f u l l y}=\lambda_{\mathcal{H}} \mathcal{L}_{\mathcal{H}}+\lambda_{\mathcal{M}} \mathcal{L}_{\mathcal{M}}+\lambda_{\mathcal{J}} \mathcal{L}_{\mathcal{J}}$($\lambda_{\mathcal{H}}=0.5, \lambda_{\mathcal{M}}=1, \lambda_{\mathcal{J}}=1$)联合训练stacked hourglass网络, residual网络和the Graph CNN。

Weakly-supervised Fine-tuning

Depth Map Loss：

$$\mathcal{L}_{\mathcal{D}}=\operatorname{smooth}_{L 1}(D, \hat{D}), \hat{\mathcal{D}}=\mathcal{R}(\hat{\mathcal{M}})$$

若只用Depth Map Loss，可发现它会导致恶化的结果，因为depth map只会给看得到的那部分表面加以限制，并且对捕捉到的depth map的噪声很敏感，所以Pseudo-Ground Truth Mesh Loss也相当有必要。所以就先用之前预训练的网络和heat-maps的真值在真实场景训练数据上运行，生成“假”的mesh真值。进过发现，这个“假”的真值具有较好的边长度和好的表面光滑度，所以弱监督部分的mesh loss只有edge loss和Laplacian loss。

Pseudo-Ground Truth Mesh Loss：

$$\mathcal{L}_{p \mathcal{M}}=\lambda_{e} \mathcal{L}_{e}+\lambda_{l} \mathcal{L}_{l}, \text { where } \lambda_{e}=1, \lambda_{l}=50$$

所以总的弱监督loss为：

$$\mathcal{L}_{\text {weakly}}=\lambda_{\mathcal{H}} \mathcal{L}_{\mathcal{H}}+\lambda_{\mathcal{D}} \mathcal{L}_{\mathcal{D}}+\lambda_{p \mathcal{M}} \mathcal{L}_{p \mathcal{M}}$$

where $\lambda_{\mathcal{H}}=0.1, \lambda_{\mathcal{D}}=0.1, \lambda_{p \mathcal{M}}=1$

另：coarsen及finner过程