读书笔记 - 计算机视觉入门介绍

虽然之前对计算机视觉已经有所了解，但是总是没有系统的学习过计算机视觉，所以这次的暑假学习中，将《A Practical Introduction to COMPUTER VISION WITH OPENCV》这本书放到了第一个，学习了一个月之后，在这篇博客中归纳学习到的内容，内容根据书中的顺序进行安排。

Introduction

计算机视觉是由计算机进行的，自动分析图像和视频的过程。它最初根据人类的视觉系统而来，由于人类的视觉系统几乎是出于自然的条件反射，所以最开始人们也认为计算机视觉是一个直截了当的问题，但是事实上，无论是人类的视觉系统，还是计算机视觉的难题都比想象的要更加复杂。

A Difficult Problem

对于计算机视觉的研究来说，首先要知道，这是一项很难的任务，对于计算机来说，图像就是一组值，计算机视觉就是要了解（understand）这一组值，而事实就是这一组值很大，很复杂，而且时刻在变化。

The Human Vision System

人们对于计算机视觉，首先想到的是，能否直接复制人类的视觉系统来解决这一问题，但问题是我们目前还不清楚人类的视觉系统大多数时刻在干些啥。
首先对于眼睛来说，颜色视觉（6–700万个视锥细胞）集中在眼睛的中心，而其余的由1.2亿个视杆组成。所以在某种成都下，我们可以认为我们看到的，是一个连续的（continuous）图像（没有blind spot盲点），图像中各处都有颜色，但是目前我们也还不清楚这种印象如何在大脑中发生。
尽管我们现在能根据电子信息的活动，判断大脑的各部位负责什么任务，但是这也不能为我们提供解决计算机视觉问题的算法或思路。

Practical Applications of Computer Vision

计算机视觉在工业中有许多应用，特别是在生产线上自动检查制成品。 例如，它已用于质量检测，生物安全识别，车牌识别等。

The Future of Computer Vision

尽管现在计算机视觉已经有很大的发展，但是仍有不足，比如现在仍然很难生产出可以在小路上行驶的可靠车辆，甚至同时也面临法律问题，如果车辆撞车，谁来负责？另外如果我们开发出一种医学成像系统来诊断癌症，而错误地没有诊断出病情时会发生什么？即使该系统可能比任何医师都更可靠，但是还是会进入法律的雷区。所以最简单的解决方案要么是仅解决非关键性问题，要么开发系统来作为当前人类专家的助手，而不是替代人类专家。另外有可能遇到的问题比如，在某些国家/地区，摄像机的安装和使用被视为侵犯了基本隐私权。
所以在未来，我们希望计算机视觉能在更自由更复杂的环境中发挥作用，比如自动驾驶，协助抓贼等等。
而计算机视觉的最终目的，是模仿人类视觉的能力，并将这些能力提供给类人机器人（和其他）机器人设备。虽然我们都有自己的良好的视觉系统，但是我们仍然希望自动的实现任何的计算机视觉任务。

Images

计算机视觉最重要的因素之一是图像，因为它为计算机提供了场景的视觉上的表示，以便计算机后续处理来突出感兴趣的特征，最后提取出信息。

Cameras

标准的相机由一个感光图像平面（photosensitive image plane）（可感应落在平面上的光量），一个防止杂散光掉落到感光图像平面上的外壳（housing），以及一个镜头罩（lens）组成，镜头允许部分光落图像平面上（镜头能通过控制透镜，将光线聚焦到图像平面上）。

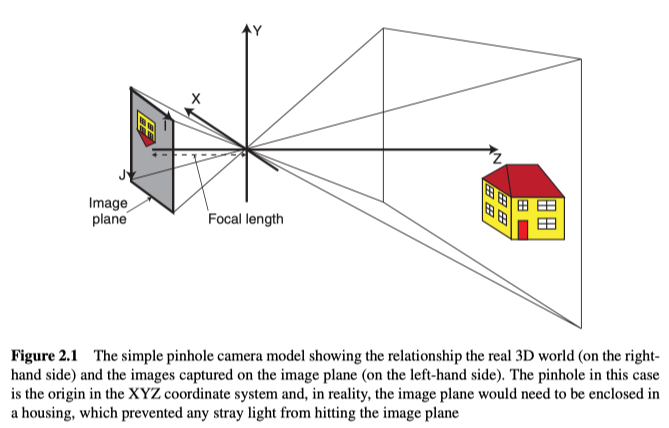
The Simple Pinhole Camera Model

最简单但合理的模型是针孔照相机模型，如图2.1所示，模型中镜头化简为针孔。该模型是大多数实际成像系统的简化，因为实际系统的各个部分都会在生成的图像中引入失真（变形）。其中从3D世界中的点（x，y，z）到图像平面上的点（i，j）的映射可以建模为：

$$\left[\begin{array}{c} i . w \\ j . w \\ w \end{array}\right]=\left[\begin{array}{ccc} f_{i} & 0 & c_{i} \\ 0 & f_{j} & c_{j} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \end{array}\right]$$

其中$w$为尺度因子，$f_i$和$f_j$是相机的焦距和像素大小的结合，$（c_i，c_j）$是与图像平面垂直且经过针孔的线与图片平面相交的点的坐标。

Images

图像是由传感器捕捉到的画面（通常是3D场景的2D投影）。而且图像可以看做是图像平面上的，关于两个坐标（（i，y）或（column，row））的连续函数，但是如果要在电脑上处理这样的图像，它必须经过一下操作：

1. 采样。从传感器信息中采样，并输入一个M×N的矩阵中。
2. 量化。矩阵中的每个元素都需要设置成整数，所以连续空间被分成一些间隔（通常为256）。

Sampling

图像本来应该是连续的，尤其是对于人眼来说，但是对于电脑来说，它会将连续图像采样到离散的元素中来创建数字图像，以便电脑处理。而数字图像的传感器由2D的光敏元件阵列组成，且每个元件（像素点/采样点/图像点）只在一定的固定区域上是光敏的，点之间的边缘区域则不是光敏的，所以传感器会丢失掉这部分的信息（比如远处的物体恰好落在缝隙）。但采样更重要的问题是，该像素代表了离散区域的平均值（亮度/色度），这在现实世界中，可以从单个物体中折射过来，也可能是多个物体反射光的总和。
显而易见，像素点的数量会影响分辨率，见图2.2所示，从而限制图像中能识别出的对象，但是过多的数量又会带来超过需求的细节，使处理变的困难，因此需要权衡。

Quantisation

函数$f(x，y)$表示了每个像素的亮度，亮度本应该是连续的，但是我们需要整数值，因此需要离散的表示，通常每个通道的亮度的级别有$k=2^{b}$个，其中b表示比特数（通常为8），b越大，储存图像所需的内存越大，但是越少，信息会丢失，所以实际上取决于储存的图像的目的，通常需要比预期更高的量化级别。

Colour Images

灰度（单色）图像只有一个通道，只能表示每个点的亮度，而彩色（多光谱）图像具有多个通道，能同时表示场景中的亮度和色度（颜色信息）。 因此，同样的采样和量化下，彩色图像比灰度图像更大，更复杂。而我们总是需要利用彩色图像的多个通道，所以我们必须以某种方式决定如何处理每个信息通道。（也有许多图像处理是专门为灰度图像开发的。）
事实上是，由于人类也能理解灰度图像，且灰度图像更小更简单，所以计算机视觉多年来都一直基于灰度图像。但是颜色确实能通过更有用的信息帮助完成图像分割，物体分类等任务。
另外人类对于波长为400nm~700nm之间的光敏感，所以大多数相机的传感器被设计为对这些波长敏感，另外彩色图像通常使用三通道的色彩空间进行表示，如下所示。

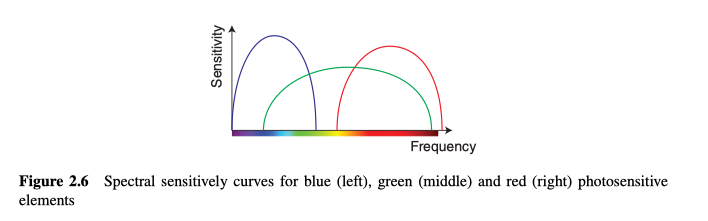
Red–Green–Blue (RGB) Images

彩色图像的最常见表示形式是使用三个通道，它们大致对应于红色（700 nm），绿色（546.1 nm）和蓝色（435.8nm）波长。这意味着照相机中的感光元件对以这些颜色为中心的波长才具有光谱敏感性（如图2.6）。

值得注意的是，由于量化，尽管该色彩空间有1680万多种（256*256*256），有些颜色仍无法表示。
RGB颜色信息可以转换为灰度图：

$$Y=0.299 R+0.587 G+0.114 B$$

另外，感光平面上的一个位置只有一个元件，一个元件只对一种波长有光谱敏感性，所以对不同波长感光的元件并非位于同一位置，而是以规则模式显示，如图2.7所示，而RGB值则是以某种方式，从这些感应值内插得到。这意味着接收到的图像甚至不是连续图像的正确采样（错位），而是从传感器元件接收到的数据中插入得到的。

Cyan–Magenta–Yellow (CMY) Images

CMY模型基于二次色（secondary colour，通过混合两个主次色得来）（RGB是主次色），其中C，M和Y的值，通过从纯白色中减去R，G，B的值得来。 所以，它通常在以白色为起点的打印机中用作颜色模型。

$$C=255-R, \quad M=255-G, \quad Y=255-B$$

YUV Images

YUV颜色模型用于模拟电视信号（PAL，NTSC…），它由亮度（Y）以及两个颜色分量组成：蓝色减去亮度（U）和红色减去亮度（V）。 从RGB的转换方程如下：

• $Y=0.299 R+0.587 G+0.114 B$
• $U=0.492^{*}(B-Y)$
• $V=0.492^{*}(R-Y)$

人类的视觉系统对亮度比对色度更加敏感，而电视信号的编码需要以减少传输的数据量为目的，所以会用到这个色彩空间。

Hue Luminance Saturation (HLS) Images

HLS模型在计算机视觉中经常使用，因为它除了将亮度和色度分开外，还将色度分为色相和饱和度，所以能够更加贴切的描述（例如深蓝色，浅红色等）。通常来说，亮度在0到1之间，色相描述了颜色，在0到360°之间，饱和度S是颜色的强度或纯度，在0到1之间。但在实际实现中，这些量会映射到到0到25​​5的范围（OpenCV内，色相值的范围是0到179）。直观的色彩空间的显示如图2.10。

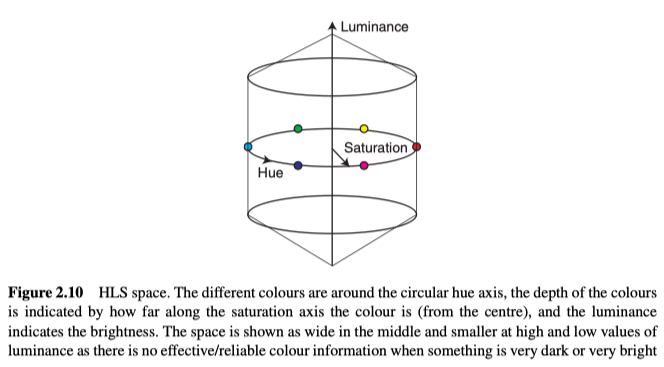
从图2.10中可以明显发现，色相轴的圆形性质，这意味着最小（0）和最大（179）的色相值仅相差1，所以它们在颜色上没有太大区别，都对应于红色像素，但是单单看色相图，一个是黑色一个是白色，这意味着，如果要处理色相通道，则必须格外小心。例如，如果0、178、1、177和179的平均色相值应为179，而不是107。
另外，RGB和HLS之间的转换方程如下（RGB都被规范化到0.0和1.0之间）：

$$\begin{array}{l} L=\operatorname{Max}(R, G, B)+\operatorname{Min}(R, G, B) / 2 \\ S=\left\{\begin{array}{ll} \operatorname{Max}(R, G, B)-\operatorname{Min}(R, G, B) / \operatorname{Max}(R, G, B)+\operatorname{Min}(R, G, B) & \text { if } L<0.5 \\ \operatorname{Max}(R, G, B)-\operatorname{Min}(R, G, B) / 2-(\operatorname{Max}(R, G, B)+\operatorname{Min}(R, G, B)) & \text { if } L \geq 0.5 \end{array}\right. \\ H=\left\{\begin{array}{ll} 60 .(G-B) / S & \text { if } R=\operatorname{Max}(R, G, B) \\ 120+60 .(B-R) / S & \text { if } G=\operatorname{Max}(R, G, B) \\ 240+60 .(R-G) / S & \text { if } B=\operatorname{Max}(R, G, B) \end{array}\right. \end{array}$$

根据上面的公式，L和S值将在0.0到1.0之间，H值应在0.0到360.0之间。

Other Colour Spaces

OpenCV提供对其他六个颜色空间的支持（就转换功能而言）：

1. HSV。
2. YCrCb 缩放了的YUV，用于图像和视频压缩。
3. CIE XYZ 标准的参考色彩空间，其中通道响应类似于人眼中不同的圆锥响应。
4. CIE ${L}^{}$${u}^{}$${v}^{}$ CIE定义的另一种标准颜色空间，旨在提供一种感知上统一的颜色空间，其中颜色之间的差异与我们感知到的差异成比例。 $\mathrm{L}^{}$是亮度的量度，$\mathrm{u}^{}$和$\mathrm{v}^{}$是色度值。
5. CIE $\mathrm{L}^{}$ $\mathrm{a}^{}$ $\mathrm{b}^{*}$ 与设备无关的色彩空间，其中包括人类可以感知的所有颜色。
6. 拜耳（Bayer）是CCD传感器中广泛使用的模式，如果我们有原始传感器数据（即尚未插值），则使用拜耳模式。

Some Colour Applications

在某些应用中，我们需要确定哪些像素代表特定颜色。例如，要查找路标，我们会对红色，黄色，蓝色，黑色和白色特别感兴趣。我们可以通过创建用于识别特定颜色的简单公式来识别特定颜色，如以下的介绍，但应注意的是，标准本身真的太粗糙了，很容易失效，也因为该标准不是基于足够数量的图像，所以实际上应该以更严格的方式进行处理。

Skin Detection

简单的通过以下公式：

$$(Saturation >=0.2 ) AND (0.5<\text { Luminance } / \text { Saturation }<3.0 ) AND (Hue <=28^{\circ} OR Hue >=330^{\circ} )$$

将识别许多皮肤像素。 但是，很明显，这也会识别其他像素。

Red Eye Detection

同样通过以下公式：

$$(Luminance >=0.25 ) AND (Saturation >=0.4 ) AND \left.\qquad(0.5<\text { Luminance/Saturation }<1.5) \text { AND (Hue }<=14^{\circ} \text { OR Hue }>=324^{\circ}\right)$$

识别红眼像素，通过实验可以确定，这还需加以改进，但是它是识别红眼的良好起点。

Noise

图像通常会受到某种程度的噪声（噪声可以是任何会降低图像质量的因素）的影响，且这种噪声会对处理过程产生影响。总的来说，噪声能来源于环境，成像设备，电气干扰，数字化过程等。而对于噪声，我们需要能够测量它，并以某种方式对它进行校正。
首先对噪声大小的衡量标准，我们使用信噪比（the signal to noise ratio）来衡量。对于一幅图像$f(i, j)$，信噪比定义为：

$$S / \text {Nratio}=\Sigma_{(i, j)} f^{2}(i, j) / \Sigma_{(i, j)} v^{2}(i, j)$$

其中$v(i, j)$代表噪声。

Types of Noise

两种最常见的噪声类型是高斯噪声和椒盐噪声。

Gaussian Noise

高斯噪声能很好的拟合许多的实际噪声。其中，噪声$v(i, j)$被建模为一个平均值为$\mu$（通常为0），标准差为$\sigma$的高斯分布，如图2.14所示。

Salt and Pepper Noise

椒盐噪声是脉冲噪声的一种，通过对单个像素的损坏，使其亮度与周围区域的亮度差异很大，其中饱和脉冲噪声会影响图像（即，纯白色和黑色像素会破坏图像），如图2.15所示。

Noise Models

噪声必须以某种方式与图像数据结合在一起，根据噪声是与数据无关还是与数据有关可以将之分为两类。

Additive Noise

这类噪声模型用于数据独立的噪声（噪声量与图像数据本身无关），其中附加噪声模型能表示为：

$$f(i, j)=g(i, j)+v(i, j)$$

其中$g(i, j)$是原始图像，$v(i, j)$是噪声，而$f(i, j)$是实际图像。

Multiplicative Noise

这类噪声模型用于数据依赖的噪声（噪声量与图像数据本身有关），其中乘法噪声模型能表示为：

$$f(i, j)=g(i, j)+g(i, j) \cdot v(i, j)$$

其中$g(i, j)$是原始图像，$v(i, j)$是噪声，而$f(i, j)$是实际图像。

Noise Generation

为了评估消除噪声的算法，我们经常需要先模拟噪声，以便可以消除/减少噪声后，评估算法成功的程度。首先假设我们生成的噪声具有高斯分布，均值为0，标准差为$\sigma$。
我们首先确定，能从最大可能的负变化到最大可能的正变化（通常k = -255..255）之间的所有可能噪声值的概率分布$p(k)$和累积概率分布$p_cum(k)$。

$$\begin{aligned} p(k) &=e^{-k^{2} / 2 \sigma^{2}} / \sigma \sqrt{2 \pi} \quad k=-(G-1), \ldots,-1,0,1, \ldots, G-1 \\ p_{\mathrm{cum}}(k) &=p_{\mathrm{cum}}(k-1)+p(k) \\ p_{\mathrm{cum}}(-(G-1)) &=p(-(G-1)) \end{aligned}$$

累积概率分布确定后，我们就能计算图像中，每个像素的噪声值了。
对于每个像素$(x，y)$，可以设置其值为：

$$f^{*}(i, j)=g(i, j)+\operatorname{argmin}_{\mathrm{k}}\left(\operatorname{rand} 0-p_{\mathrm{cum}}[k]\right)$$

其中：

$$\begin{array}{ll} f^{\prime}(x, y)=0 & \text { if } f^{*}(x, y)<0 \\ f^{\prime}(x, y)=G-1 & \text { if } f^{*}(x, y)>G-1 \\ f^{\prime}(x, y)=f^{*}(x, y) & \text { otherwise } \end{array}$$

注意，argmin函数给出最小值的索引，在这种情况下，将在累积分布内选择值最接近随机数的k。另外，截断（为确保值保持在0到255之间）其实会稍微改变噪声的高斯性质。

Noise Evaluation

噪声的评估可以主观或客观地进行。 在主观评估中，将图像显示给观察者，观察者根据一系列标准对其进行评估并给出评分。但是在客观评估中，给定图像$f(i, j)$和已知参考图像$g(i, j)$，我们可以对它们之间差异进行度量，例如：

$$\begin{array}{l} \text { Mean Quadratic Difference }=\sum \sum(g(i, j)-f(i, j))^{2} \\ \text { Mean Absolute Difference }=\sum \sum|g(i, j)-f(i, j)| \\ \text { Or we can compute the signal to noise ratio assuming} v(i, j)=f(i, j)-g(i, j) \end{array}$$

显然，这种客观评估需要我们事先知道原始图像或添加的噪声。因此，实验中经常人为地添加噪声，以检验现有技术在去除噪声方面的表现如何。

Smoothing

消除噪声的方法有很多种，但是由于技术原理的不同或图像数据性质的不同，在不同情况下应该使用不同的技术。
其中，减少噪声最常用的方法是线性平滑变换，其中的计算可以表示为线性和，但是这样的噪声会导致锐边模糊，因此有些方法提出了非线性变换（不能表示为简单的线性和，逻辑操作等）。
注意这些技术面对像是大斑点或者后条纹，都无法起作用，这时需要用到的是图像恢复技术。

Image Averaging

如果对完全相同场景，存在多个图像，则将它们进行平均处理，就可以减少噪声。比如现有n张图像，其平均值为：

$$f^{\prime}(i, j)=\frac{1}{n} \sum_{k=1 . . n} f_{k}(i, j)=\frac{1}{n} \sum_{k=1 . . n} g_{k}(i, j)+v_{k}(i, j)$$

这种消除噪声的算法假设噪声是数据独立的。同样也假设：

• 所有图像的原始图像$g_{\mathrm{k}}(i, j)$是相同的（即场景和摄像机是静态的）。
• 每个图像中的噪声$v_{\mathrm{k}}(i, j)$之间存在统计独立性。
• 噪声$v_{\mathrm{k}}(i, j)$具有高斯分布，且均值为0和标准差为𝜎。

如果以上假设成立，那么图像平均之后，将保持高斯性质，但标准偏差将减小$\sqrt{n}$倍，如图2.16所示。

由以上假设可知，该方法不适用于椒盐噪声，且当场景非静态时，将引入模糊。

Local Averaging and Gaussian Smoothing

如果只有一个图像可用，则仍然可以执行平均，但不是全局，而是对图像中的每个点，计算以当前点为中心的像素块（而不是使用多个图像中的对应点）的平均值，最简单的比如3×3。
若每个点都均等权重，该技术称为局部平均（local averaging），也就是加入模糊效果，滤波器的蒙版越大，效果越明显。但是也可以更改权重，以便为更接近当前点的点赋予更高的权重，其中非常常见的加权方法是由高斯分布定义的。 例如，以下所示：

$$h_{1}=\frac{1}{9}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{array}\right] \quad h_{2}=\frac{1}{10}\left[\begin{array}{lll} 1 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 1 \end{array}\right] \quad h_{3}=\frac{1}{16}\left[\begin{array}{lll} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{array}\right]$$

$h_1$是一个3×3的局部平均滤波器，$h_2$和$h_3$都是3×3的高斯平滑滤波器，但前者的$\Sigma$更小。

很明显，局部像素进行平均时，会引入模糊从而降低可见的（高斯）噪声，但是它也会对边缘（灰度或颜色变化很大）产生影响，反而使图像更模糊，反而更难处理，但有时这都无可厚非，都是需要平衡的点。
值得注意的是，对于椒盐噪声，平均后，噪声也会再次平滑到图像中，局部平均滤波器并不适用于此类噪声。
另外，对于这种平均操作，通常使用卷积技术来执行，将掩码（通常为正方形且以当前点为中心）与所有可能位置进行卷积：

$$f^{\prime}(i, j)=\sum_{\mathrm{m}} \sum_{\mathrm{n}} f(i, j) \cdot h(i-m, j-n)$$

Rotating Mask

旋转遮罩是一种非线性算子，它首先分别在九个预设的包含当前点的mask内进行计算，选出其中最均匀的（即自相似的）mask，然后在mask内，应用平均滤波器。其中所有的mask如图2.19所示，其形状和大小可以变化。

对于每一个mask，我们计算与mask中的点相对应的点的局部平均值（色散）来衡量其自似性，然后选择色散最小的mask来进行平均化操作。这样的目的是减少当前点的噪声，让当前点与来自相同物理刺激（例如表面或物体）的其他类似点取平均值。
该技术可以迭代着来使用，直到没有变化或变化很小。掩码越大，收敛越快，但尽管该技术要慢得多，但它能同时抑制噪声和锐化图像边缘。其中色散可通过计算每个点的平方差的均值得来：

$$D=\frac{1}{n} \sum_{(i, j) \in M a s k}\left(f(i, j)-1 / n \sum_{\left(i^{\prime}, j^{\prime}\right) \in \text { Mask }} f\left(i^{\prime}, j^{\prime}\right)\right)^{2}$$

化简为；

$$D=\frac{1}{n}\left(\sum_{(i, j) \in \text { Mask }} f(i, j)^{2}-1 / n\left(\sum_{\left(i^{\prime}, j^{\prime}\right) \in \text { Mask }} f\left(i^{\prime}, j^{\prime}\right)\right)^{2}\right)$$

化简后，计算cost显着降低。
另外，该技术可以应用于，具有椒盐噪声的图像，但是会导致不良效果，尤其是当噪声存在于物体边缘时。

Median Filter

另一种非线性平滑操作是将每个像素替换为，以该像素为中心的小区域（例如3x3）中的像素中位值。例如，3x3区域包含像素值（25 21 23 25 18 18 255 30 13 22），排序后为（13 18 22 21 23 25 25 30 255），其中位数为23，而均值为48。可见该技术非常擅长处理噪声，且该技术不会使边缘模糊太多，所以可迭代应用。而实际上，中值滤波与旋转mask的效果非常相似。如图2.17和2.18所示。

虽然也可将其与上一个，在非矩形区域计算的技术结合，但是它还是会损坏细线和角，而且其时间复杂度为$O\left(k^{2} \log k\right)$，所以计算上也很昂贵。拓展的优化技术可看Median Filtering in Constant Time by Perreault

Histograms

一个图像的直方图是对该图像的抽象描述，其中包含了各个图像值（亮度/强度）的频率。

1D Histograms

对于灰度图像，其中灰度强度有256种（0-255），而每个强度对应的值，表示图像中属于该灰度的，有多少个像素。如图3.1所示。

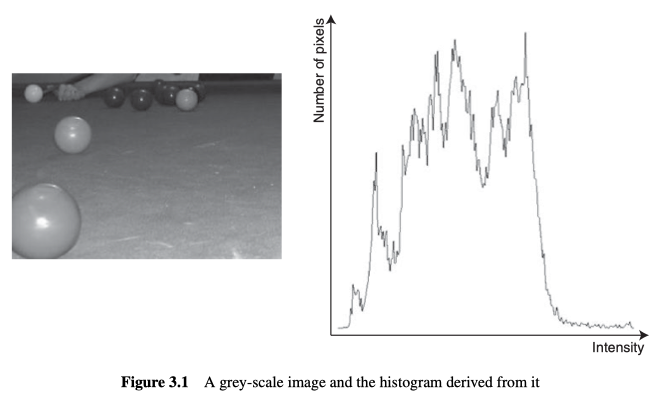
图像的直方图中包含了该图像的全局信息，并且该信息完全独立于场景中各个对象的位置和方向，所以同一直方图对应的图像不是唯一的，许多非常不同的图像可能具有相似（甚至相同）的直方图。另外，直方图中得出的信息（例如平均强度及其标准偏差）可用于执行分类。

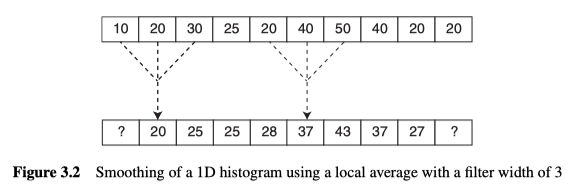
Histogram Smoothing

直方图中，无论是全局还是局部的最大值和最小值都能提供有用的信息，但是局部的极值太多了。为了减少此数字，可以对直方图进行平滑处理。首先创建一个新的直方图，其中每个值，都是以原始直方图中的相应值为中心的多个值的平均值。此过程通常称为过滤。如图3.2。

Colour Histograms

对于彩色图像这样的多通道图像来说，通常为每个通道独立确定直方图，如图3.3，图3.4。

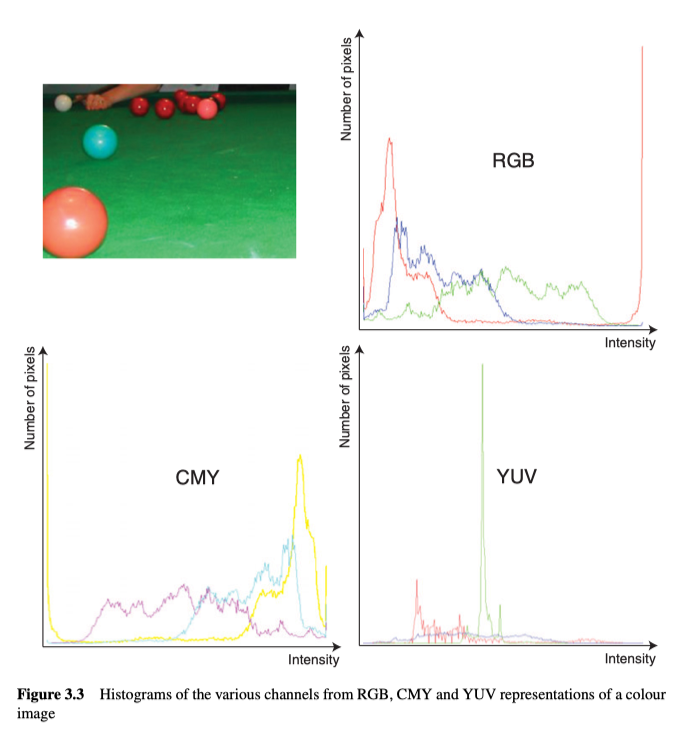
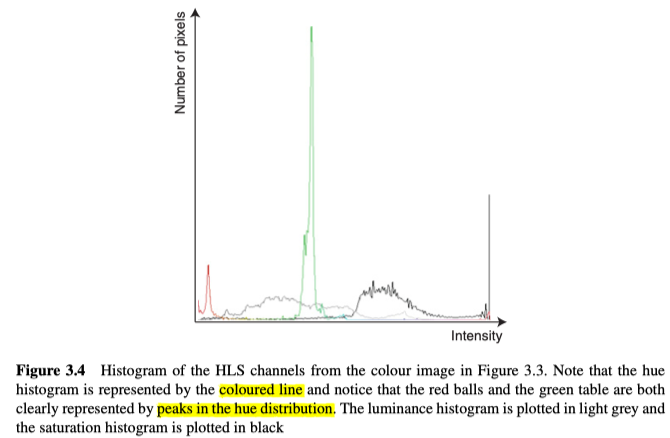
由上可知，不同的颜色模型，直方图也有很大的区别，进而对其有用性产生巨大影响。比如图3.4中可以直接发现，红色和绿色很显著。

3D Histograms

对于色彩图像的直方图处理，若是均独立处理，则不会实现最佳的颜色分割。比如相似颜色的点都具有较高的饱和度和色相值，这时需要更好的分割，则需要用到3D直方图，如图3.5。

其中，(0,0,0)点显示在左下角的顶层。绿轴从顶层的左下角到右下角，蓝轴从顶层的左下角到左上角，红轴从顶层的左下角到最底层的左下角。每个单元内显示的灰度强度表示每个单元中的相对像素数（黑色= 0，白色=最大）。
另外就是直方图中的单元数的设置。如果我们假设每个通道8位，则直方图中将有近1,680万个单元，这作为图像中信息的摘要来说太多了，所以我们需要减少了直方图的量化。比如图3.5中，每个通道只有2位，所以直方图中只有64个单元。
OpenCV中的代码可写为：

MatND histogram;
int channel_numbers[] = { 0, 1, 2 };
int * number_bins = new int[image.channels()]; 
for (ch=0; ch < image.channels(); ch++)
	number_bins[ch] = 4;
float ch_range[] = { 0.0, 255.0 };
const float * channel_ranges[] = {ch_range,ch_range,ch_range};
calcHist( &image, 1, channel_numbers, Mat(), histogram, image.channels(), a_number_bins, channel_ranges );

Histogram/Image Equalisation

在最佳观看条件下，人类可以区分700到900种灰度，但是在图像的非常黑或非常亮的区域，just noticeable difference（JND）将大大降低，人类也将很难解读图像，然而，很明显，人类更容易区分较大的差异，因此，如果改善图像中的灰度分布，这将有助于人类观察者的理解。
而改善图像中的灰度分布的一种技术是直方图均衡化，它通过在图像中均匀分布灰度，使生成的直方图变得平坦（即各个灰度具有完全相同的点数），但绝对的平坦是不可能的，实际情况是，有些像素没有值，而有较高值的灰度图散落在直方图中。见图3.6。

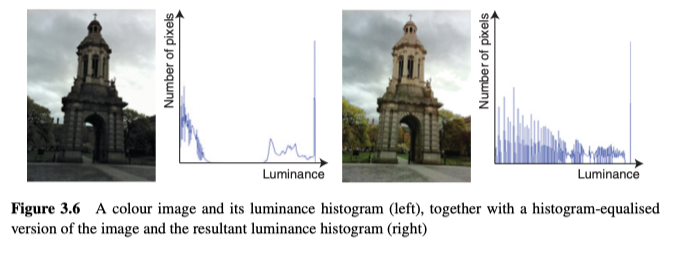
另外，对于彩色图像时，我们通常仅均衡亮度通道的直方图，以免颜色失真。

Histogram Comparison

大多数图像搜索引擎都提供了，检索与给定图像相似或包含特定内容的图像的功能，这大多数情况下是通过使用与图像关联的元数据标签实现的，但是通过分析图像中的颜色分布，也可以为该过程提供帮助，比如分析比较直方图。
用于比较直方图的指标如：

• $D_{\text {Correlation }}\left(h_{1}, h_{2}\right)=\frac{\sum_{i}\left(h_{1}(i)-\overline{h_{1}}\right)\left(h_{2}(i)-\overline{h_{2}}\right)}{\sqrt{\sum_{i}\left(h_{1}(i)-\overline{h_{1}}\right)^{2} \sum_{i}\left(h_{2}(i)-\overline{h_{2}}\right)^{2}}}$
• $D_{\text {Chi }-\text { Square }}\left(h_{1}, h_{2}\right)=\sum_{i} \frac{\left(h_{1}(i)-h_{2}(i)\right)^{2}}{\left(h_{1}(i)+h_{2}(i)\right)}$
• $D_{\text {Intersection }}\left(h_{1}, h_{2}\right)=\sum_{i} \min \left(h_{1}(i), h_{2}(i)\right)$
• $D_{\text {Bhattacharyya }}\left(h_{1}, h_{2}\right)=\sqrt{1-\frac{1}{\sqrt{\overline{h_{1}} \overline{h_{2}} N^{2}}} \sum_{i} \sqrt{h_{1}(i) \cdot h_{2}(i)}}$
  其中:
• $N$ 是直方图中的格子数(bin)
• $\overline{h_{k}}=\Sigma_{i}\left(h_{k}(i)\right) / N$

另外，也可以使用Earth Mover’s Distance，来确定将一种分布（在这种情况下为直方图）转换为另一种分布的最低路线的距离。通过迭代可以得出结果：

$$\begin{array}{c} E M D(-1)=0 \\ E M D(i)=h_{1}(i)+E M D(i-1)-h_{2}(i) \end{array}$$

最后的距离就可写为：

$$\sum_{i}|E M D(i)|$$

这也可以用在颜色直方图中。

Back-projection

上一章介绍了一些非常简单的方法来选择图像中的特定颜色。这些方法在定义它们的颜色空间中选择了相当粗糙的子空间。解决此问题的更好方法如：

1. 获取要选择的颜色的代表性样本集（类似颜色的照片切片）。
2. 根据这些样本创建直方图。
3. 将直方图标准化，使其最大值为1.0，这样就可以将直方图的值视为概率（即，具有相应颜色的像素来自样本集的概率）。
4. 将归一化后的直方图反向投影到，需要计算图像中的每个像素与样本集的像素的相似度的图像中，也就是得出了一个概率图$p$，其中$p(i, j)$表示$f(i, j)$像素和对应样本集之间的相似性，即$p(i, j)=h(f(i, j)))$。

k-means Clustering

颜色的一个主要问题是它种类太多了（例如8位RGB空间就有1680万种颜色），所以通常会希望减少此数字，来更真实的压缩图像，或者表示某人穿着的衣服的颜色。为了实现这种效果，一种常用的技术是在3D颜色空间中进行聚类（例如，参见图3.9中使用的原始的k均值聚类算法）。

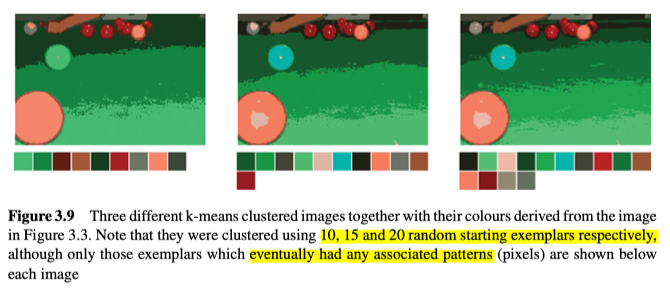
该算法的目的，是找出k个示例（即特定颜色）来最好地表示图像中的所有颜色，这个k是超参数，是预先指定的。图像中的每个像素的颜色称为pattern、图案。而与特定的exemplar、范例（k个示例之一）关联的一组pattern，称为一簇。操作如下：

• 起始exemplar可以来源于：
  • 随意选择
  • 选择最开始的k个pattern
  • 均匀的分布
• 第一轮：对于所有pattern，将其分配给最近的exemplar。在每个新pattern都被关联之后，计算与exemplar相关联的所有pattern的重心，并将之作为新的exemplar。
• 第二遍：使用第一遍得到的新的exemplar，然后给所有pattern根据距离重新分配给exemplar（这些分配可能与上次不同）。

对k聚类算法的简单的一维展示如图3.10所示：

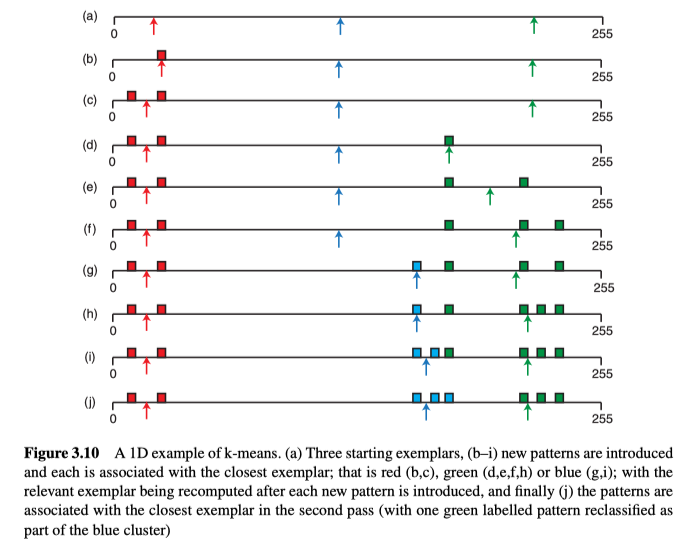
注意，由于每次起始样本的选择都是随机的，所有该算法是不确定的，所有每次执行都会有不同的结果。另外对于一个区域，用多少种颜色来表示并不容易，比如在图3.9中，只有右侧的图像才能真实地再现每个斯诺克球的颜色，所以如何才能确定，用多少个颜色（k）再现区域会更加合适呢？
一种方法是看哪个聚类数的输出结果具有最高的置信度，置信度可以使用诸如Davies-Bouldin指数之类的指标：

$$\mathrm{DB}=1 / \mathrm{k} \sum_{1 . . \mathrm{k}} \max _{i \neq j}\left(\left(\Delta_{\mathrm{i}}+\Delta_{\mathrm{j}}\right) / \delta_{\mathrm{i} . \mathrm{j}}\right)$$

它考虑了k个聚类，并对聚类之间的分离度求和。具体来说，对于每个簇，都使用以上公式，找到与之最不分离的另一个簇。以上公式对于任何两个簇，分别计算两个簇到各自的簇中心的平均距离之和（Δi +Δj），再除以簇之间的距离，得到分离度。尽管此指标是簇中最常用的指标之一，但由于它没有考虑簇的大小，因此在簇的大小不一的情况下效果不佳。

总的来说，k均值聚类是无监督学习的一个示例，即从现有的数据中学会了划分方式。其中非监督学习是指学习过程中，不会收到分类是否正确的反馈的学习，它必须基于输入数据的内部规律，来让相似的事件/像素点/物体，以相同方式被分类。

Binary Vision

灰度图像的每个像素通常有8位，尽管在某些方面，它处理起来会比彩色图像更容易，但是存在一种比灰度图像更简单的图像形式（即二进制图像）。实际上，计算机视觉已经有很大一部分的实际应用基于二元图像。

Thresholding

通过对灰度图像进行阈值处理，能得到二元图像。算法很简单：

$$\begin{aligned} \text{For all pixe} & \text{ls} (i, j) \\ f^{\prime}(i, j) &=1 \text { where } f(i, j)>=T \\ &=0 \text { where } f(i, j)<T \end{aligned}$$

二元图像的灰度值并非二进制的0和1，而通常使用灰度值0和255代替，所以可以使用8位的格式表示结果图像，进而可以用与原始灰度图像相同的方式来显示和处理。
虽然可以逐元素判断其值是否超过阈值，但最有效的方法（通常可以在硬件中完成）是使用查找表。

$$\begin{aligned} \text{For all grey lev} &\text{els } k = 0 \text{. . .} 255 \\ \operatorname{LUT}(k) &=1 \text { where } k>=T \\ &=0 \text { where } k<T \\ \text{For all pixels } (i&, j) \\ g(i, j) = &\operatorname{LUT}(f(i, j)) \end{aligned}$$

通常使用阈值操作以便将某些感兴趣的对象与背景分离，且通常将感兴趣的部分用1（或255）表示，但有时需要反转二进制图像才能如此。

Thresholding Problems

若要使用阈值技术，首先，要分离开的前景和背景必须是不同的。如果它们没有区别，将很难（甚至不可能）使用阈值技术来准确地对其进行细分。但也有许多技术（比如自适应阈值）来尝试处理前景和背景的区别不明确的情况，和许多技术（例如腐蚀，膨胀，打开，关闭） 来改善分割不完美的二值图像。

Threshold Detection Methods

即使在某些工业化的密闭场景，随着时间的推移，其照明条件也会发生变化，其光源也会随着时间逐渐变弱，若只是凭借一开始手动设置的阈值，就可能会引起问题。因此，需要一种机制来自动的确定阈值。
在以下内容中，我们假设有一个灰度图像$f(i, j)$，它的直方图为$h(g)=\sum_{i, j}\left[\begin{array}{l}1 f(i, j)=g \\ 0 \text { otherwise }\end{array}\right.$，再将之转换为概率分布$p(g)=h(g) / \sum_{g} h(g)$。

Bimodal Histogram Analysis

图像的阈值可以通过分析其直方图而来。现在我们假设，图像的背景主要集中于一个灰度值，而前景主要集中于另一个灰度值，那进而可以假设直方图是双峰的（即具有两个主峰）。然后，要计算阈值，我们可以简单地寻找anti-mode、反模式（峰值之间的最小值）。

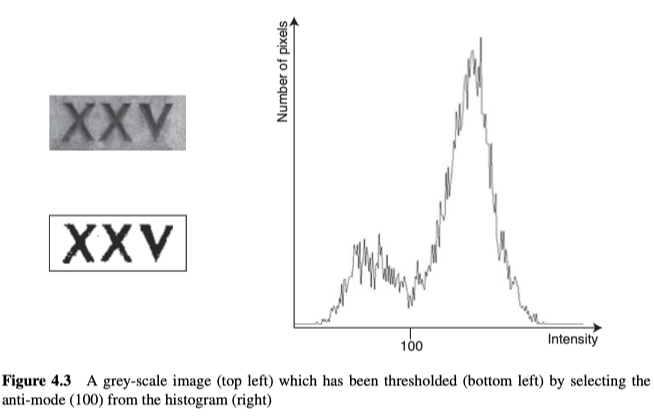
但是，如图4.3所示，虽然直方图整体上是双峰的，但它同时也存在许多局部的最大值和最小值，所以要找到反模式其实并不容易。一般有以下几种方法来解决此问题时：

• 首先使直方图平滑（来抑制噪声的峰值）
• 使用可变的步长来找反模式（而不是将每个直方图的每个模式都考虑到）
• 忽略梯度高的点（因为这些点代表了边界），从而更好的分割直方图的两种模式
• 仅仅对边界点绘制直方图，然后直接获取直方图的模式，即为反模式。

然而，以上这些方法有时会造成反模式的偏移，从而产生不好的阈值。所以接下来介绍其他基于直方图的更为可靠的方法。

Optimal Thresholding

以上的技术，适用于模式合理地分开并噪声不太大的情况，但是当模式之间的距离越来越近时，首先反模式就不再是最佳解决方案。如图4.4中的两个正态分布及其求和所示。

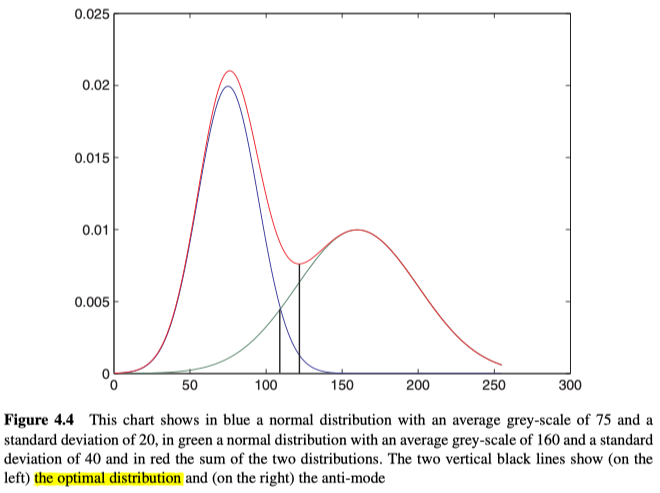
其最佳阈值应该是两个正态分布相交的位置（左侧垂直线），但这时总分布的反模式位于右侧（右侧垂直线）。
综上所述，如果我们可以将直方图，建模为两个正态分布（但可能重叠）的总和，那么可以使用一种称为“Optimal Thresholding、最佳阈值”的算法，该算法没有直观的解释其原理，但它不断的迭代，将产生最终结果。
算法如下：

1. 设置$t$为0，$T^t$=<一些初始的阈值>
2. 根据当前阈值$T^t$，计算前景和背景的平均值 $$\begin{array}{ll} w_{\mathrm{b}}\left(T^{t}\right)=\sum_{g=0}^{T^{\prime}-1} p(g) \quad \mu_{\mathrm{b}}\left(T^{\prime}\right)=\Sigma_{g=0}^{T^{\prime}-1} p(g) \cdot g / w_{\mathrm{b}}\left(T^{\prime}\right) \\ w_{\mathrm{f}}\left(T^{t}\right)=\sum_{g=T^{\prime}}^{255} p(g)=1-w_{\mathrm{b}}\left(T^{t}\right) \quad \mu_{\mathrm{f}}\left(T^{\prime}\right)=\sum_{g=T^{\prime}}^{255} p(g) \cdot g / w_{\mathrm{f}}\left(T^{\prime}\right) \end{array}$$
3. 设置$T^{t+1}=\left(\mu_{\mathrm{b}}\left(T^{t}\right)+\mu_{\mathrm{f}}\left(T^{t}\right)\right) / 2$以及将t增加1，为下一迭代更新阈值
4. 回到第二步，直到$T^{t+1}=T^{t}$

重要的是，设置的初始值必须能让某些对象和某些背景像素分离，否则算法将因除零错误而失败。另外，只有当直方图满足“两个正态分布的和的”假设时，该算法输出的结果才是最佳的选择。

Otsu Thresholding

Optimal Thresholding 所假设的条件，通常不会成立，这时它的结果可能不可接受，所以Otsu定义了另一种方法，将阈值两边的像素值的分布最小化：

考虑所有可能的阈值，并选择能使类方差$\sigma_{W}^{2}(T)$最小的阈值T：

$$\sigma_{W}^{2}(T)=w_{\mathrm{f}}(T) \sigma_{f}^{2}(T)+w_{\mathrm{b}}(T) \sigma_{b}^{2}(T)$$

其中$w_{\mathrm{f}}(T)$和$w_{\mathrm{b}}(T)$分别是属于前景和背景部分的点，$\sigma_{f}^{2}(T)$和$\sigma_{b}^{2}(T)$分别是前景和背景灰度值的方差：

$$\begin{array}{ll} w_{f}(T)=\sum_{g=T}^{255} p(g) & \sigma_{f}^{2}(T)=\sum_{g=T}^{255} p(g) \cdot\left(g-\mu_{f}(T)\right)^{2} / w_{\mathrm{f}}(T) \\ w_{\mathrm{b}}(T)=\sum_{g=0}^{T-1} p(g) & \sigma_{b}^{2}(T)=\sum_{g=0}^{T-1} p(g) \cdot\left(g-\mu_{b}(T)\right)^{2} / w_{\mathrm{b}}(T) \end{array}$$

其中$\mu_{f}(T)$和$\mu_{b}(T)$分别是前景和背景的灰度值的均值。

$$\mu_{f}(T)=\sum_{g=T}^{255} p(g) \cdot g / w_{\mathrm{f}}(T) \quad \mu_{b}(T)=\sum_{g=0}^{T-1} p(g) \cdot g / w_{\mathrm{b}}(T)$$

让类里方差最小的阈值也是能让类之间方差$\sigma_{B}^{2}(T)$最大的阈值，这是因为$\sigma_{B}^{2}(T)=\sigma^{2}-\sigma_{W}^{2}(T)$，其中$\mu$和$\sigma^{2}$是图像数据的均值和方差。
给两个类$f$和$b$，其类之间方差为：

$$\sigma_{B}^{2}(T)=w_{f}(T)\left(\mu_{f}(T)-\mu\right)^{2}+w_{b}(T)\left(\mu_{b}(T)-\mu\right)^{2}$$

进而简化为：

$$\sigma_{B}^{2}(T)=w_{f}(T) w_{b}(T)\left(\mu_{f}(T)-\mu_{b}(T)\right)^{2}$$

其中$\mu=w_{f}(T) \mu_{f}(T)+w_{b}(T) \mu_{b}(T)$
所以总的来说，就是遍历所有可能的阈值T，找到能使上式的类间方差最大的阈值，即为结果，可以看出我们只需计算前后部分的权重和均值，就能作出判断。

Variations on Thresholding

Adaptive Thresholding

以上出现的技术中，都对全局进行阈值处理（即，将单个阈值应用于图像中的所有点）。但在某些情况下，也可以使用多个阈值来更好的改善阈值结果。

比如图4.7，其中若只用单个的全局最佳阈值，图中的大部分书面细节将消失。而使用自适应阈值处理（具有64个阈值/图像块），大多数细节都可以正确显示。其中，自适应阈值算法为：

1. 将图像划分为多个子图像（如在图4.7中，用8×8网格分割成64个子图像）。
2. 对于每个子图像，分别计算阈值。
3. 对于图像中的每个点，使用双线性插值从四个最近的阈值中插值一个阈值来确定该点的阈值。

图4.7中可发现，该技术并非在所有地方都能正常工作，比如有两个黑色区域，对于这种情况，可以给全局的各个阈值添加限制来解决，以确保阈值在整个图像没有明显的变化。
重要的是，在OpenCV中，该技术并非本文介绍的那样，它计算的是当前像素，与以当前像素为中心的，block_size大小的像素块的局部平均值之间的差异，如果差异减去offset之后比0大，则设置输出值为255，反而设置为0，其中block_size对输出有很大影响，另外，也可以使用高斯加权平均值来代替局部平均值。实际上，基于局部区域的均值，相当于以另一种方式得到了当前像素的新阈值。

Band Thresholding

Band Thresholding使用了两个阈值，一个在对象/物体的像素以下，另一个在对象/物体的像素以上：

$$\begin{array}{ralign} \text{For all pixels } & (i, j) \\ f^{\prime}(i, j)&= 1 \text { for } f(i, j) \geq T_{1} \text { and } f(i, j) \leq T_{2}\\ &= 0 \text { otherwise} \end{array}{}$$

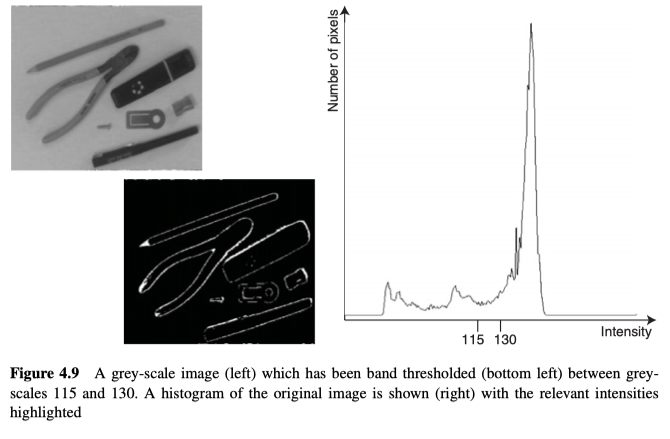
如图4.9所示，该技术可以用于定位物体/对象的边界，虽然对于边界，边缘检测器会更可靠，更合适。

Semi-Thresholding

半阈值化，对物体像素保留其原始灰度值，但将其背景像素设置为黑色。

$$\begin{array}{ralign} \text{For all pixels } & (i, j) \\ f^{\prime}(i, j)&=f(i, j) \text { for } f(i, j) \geq T\\ &= 0 \text { otherwise} \end{array}{}$$

结果图如图4.10所示。

Multispectral Thresholding

对于彩色图像，如果要应用阈值，最常见的做法是将图像转换为灰度，然后转换为阈值，不过也可以对每个通道独立应用阈值（如图4.11所示），甚至还可以在3D颜色空间内进行阈值设置（比如，如果一个像素的颜色，存在于3D色彩空间的特定子空间中，则将该像素定义为对象/物体像素）。

Mathematical Morphology

数学形态学是一种，基于set operations、运算集的图像处理方法，这些运算集通常对物体的形状，进行非线性算子的代数运算。它提供了许多描述图像处理和分析操作的统一框架，并让一些很难描述的技术（以下内容）的开发成为可能。
其中，形态运算将structuring elements、结构元素有效地移动到图像中的每个可能的位置，并分别进行逻辑运算（以某种方式将结构元素与图像进行比较），并将运算结果存储在单独的输出图像中。

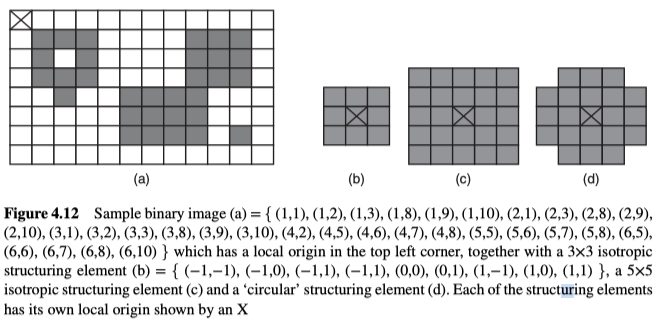
操作过程中，将二值图像看作2D的网格，对象点就是网格中的点，且网格原点与原图的原点相同（如图4.12（a）所示）。而结构元素通常是围绕它们自己的原点（通常对称）定义的少量的对象点集。典型的结构元素是各向同性的（矩形中的所有点都属于结构元素），比如图4.12（b）和（c），但它不必是各向同性的，如图4.12（d）。

Dilation

膨胀是一种用于扩展物体/对象的像素数量的技术，如图4.13所示，它通常会同时在所有方向上扩展：

$$X \oplus B=\left\{p \in \varepsilon^{2} ; p=x+b, x \in X \text { and } b \in B\right\}$$

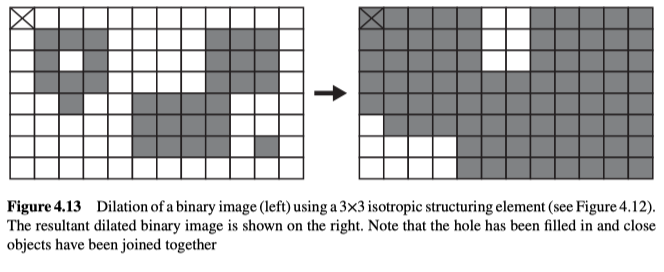
它将二值图像X中的每一个对象点x，转换为结构元素B中的每一个对象点b（相对于结构元素原点的对象点向量），所以图像X中的每一个对象点都能造成输出图像中出现一些对象点，但重复项不保留。
膨胀会增加物体的大小（即集合中的点数），从外观上来看，它会导致小孔被填充，并将较大的对象块之间的狭窄间隙填满。另外，一般用于图像中的扩散使用各向同性的结构元素。

Erosion

侵蚀是一种通过消除边界上的像素点，来缩小对象/物体形状的技术，如图4.15所示：

$$X \ominus B=\left\{p \in \varepsilon^{2} ; p+b \in X \text { for every } b \in B\right\}$$

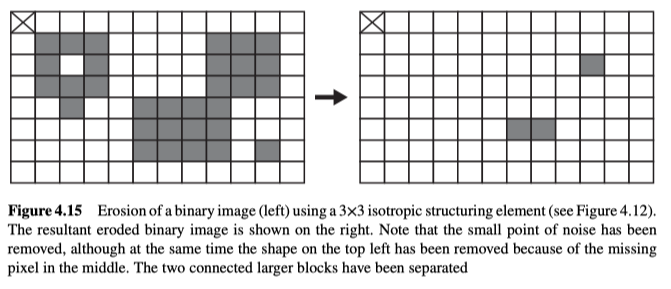
由图可知，当且仅当为当前点转换时，结构元素所对应的所有点都是对象点，该点才是侵蚀输出集的元素，也可将其视为匹配问题，将结构元素与输入图像的每个可能位置进行匹配，只有完美匹配的点，才能被标记输出。
此操作会减少了对象的大小（即集合中的点数），即，消除任何小的噪声点，以及任何狭窄的特征。与膨胀类似，侵蚀一般也使用各向同性的结构元素。

Opening and Closing

侵蚀可以看做是膨胀的镜像，反之亦然，一个扩大对象像素的数量，另一个缩小对象像素的数量，将这些操作结合在一起，就是开运算和闭运算。
开运算是先侵蚀再膨胀的操作，使用的结构元素相同：

$$X \mathrm{O} B=(X \ominus B) \oplus B$$

开运算可以消除噪点（消除比结构元素小的图像细节），以及较窄的特征（例如较大对象块之间的连接），并平滑对象边界。与侵蚀和膨胀不同，它能近似保持物体的大小。
而闭运算是先进行膨胀操作，再进行侵蚀操作，使用的结构元素相同：

$$X \cdot B=(X \oplus B) \ominus B$$

闭运算能连接互相接近的对象，并填充对象内的孔。它倾向于使对象的形状有些变形，但也能近似保持物体的大小。
在许多应用中，通常会先进行一个闭运算然后进行一个开运算，来搭理二值图像，如图4.17和图4.18。

Grey-Scale and Colour Morphology

除了二值图像，形态学运算也可以应用于灰度和彩色图像。在这些情况下，各个通道上的每个不同的灰度层级（level）都被单独视为一个集合（即，所有大于或等于特定灰度级别的点），如图4.19所示。图4.20和图4.21，分别是对灰度图像以及颜色图像进行开运算和闭运算的示例。

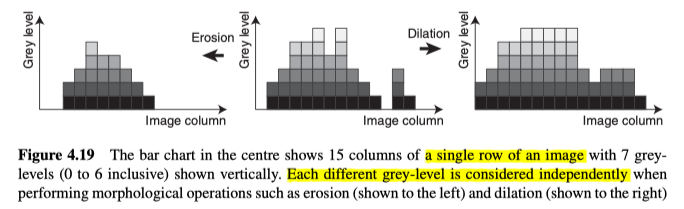
具体来说，可以理解为，对给定像素进行结构像素的匹配，找到对应区域的最小值或最大值，膨胀的公式如下：

$$\delta_{B}(f)_{x}=(f \oplus B)_{x}=\max _{\beta \in B} f(x+\beta)$$

侵蚀的公式如下：

$$\varepsilon_{B}(f)_{x}=(f \ominus B)_{x}=\min _{\beta \in B} f(x+\beta)$$

开运算和闭运算不再赘述。

Connectivity

在进行阈值处理以及噪声清理后，就需要在场景中定位对象了，而定位则需要确定哪些像素实际连在一起，如图4.22所示。

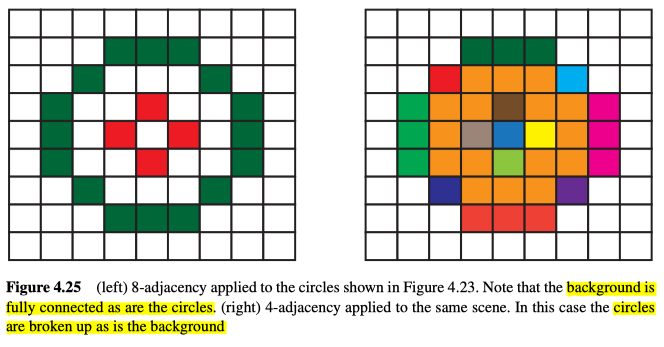
Connectedness: Paradoxes and Solutions

见上图左边，可以发现，两条线虽然相交，表现为连续的，但是并不属于同一部分，而右边可以发现，两个似乎连续的两个圆，在同样似乎连续的背景上。这两个图展示了可能会遇到的一些问题，虽然在二值图中，右边的图才更有意义。
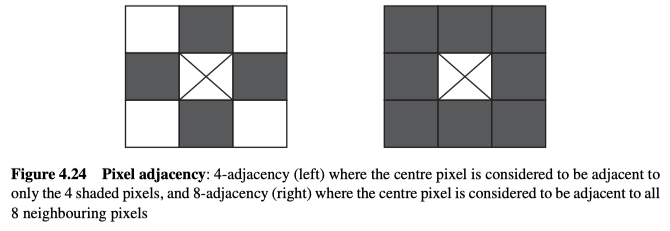
在确定哪些像素相邻时，首先要选择两种方案：4邻接，仅将东、南、西、北的像素视为相邻；以及8邻接，将所有直接围绕的像素视为相邻，见图4.24所示。

从理论上讲，我们希望使用像素的相邻性，来构建连续的整块区域，既区域中的任意两个点都可以用属于该区域的点连接起来。此类区域，相对于背景而言也就是对象/物体（有可能含有孔）。但是对于图4.23中的圆来说，无论是4邻接还是8邻接都无法得到预期的结果，如图4.25所示。

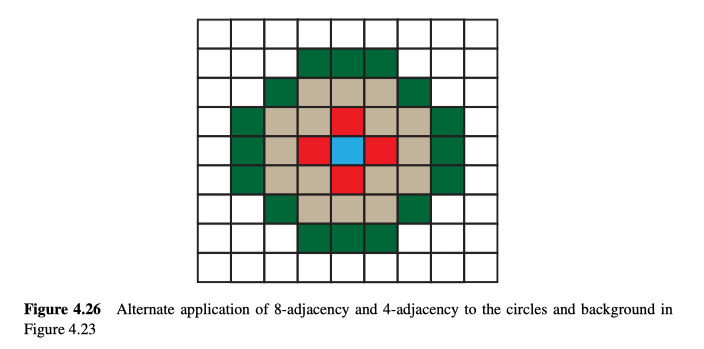
解决此问题的一种思路是，同时使用4邻接和8邻接：

• 对于外部背景使用4邻接原则。
• 对于外部物体/对象使用8邻接原则。
• 对于孔使用4邻接原则。
• 对于孔中的物体使用8邻接原则。

效果如图4.26所示。

Connected Components Analysis

在解决了连通性悖论后，需要一种实用的算法来给每个像素贴标签，这里的像素仅指二值图像中的对象像素，所以不用担心连接性问题，故可以仅使用8邻接和4邻接的其中一个来为像素贴标签（因为基于先前的相邻像素），见图4.27。

算法如下：

1. 在图像中逐行搜索，并在每行里逐列搜索：
   对于每个非零的像素：

    如果所有先前的相邻像素，都是背景像素：
        给当前像素赋予新的标签
    否则：
        从先前的相邻像素的标签中,任选一个作为当前像素的标签
        如果任何两个先前的相邻像素之间有不同的标签：
            将这些标签记下为等效的
   

2. 遍历整个图像，将等效的标签都设置为相同的标签值。

算法说明见图4.28，效果见4.29。

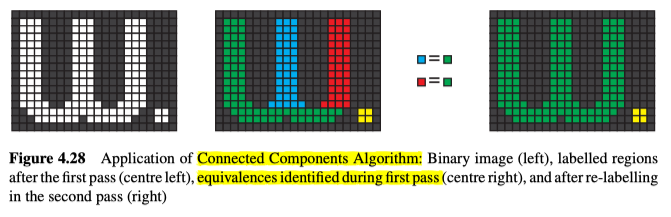
总的来说，我们用阈值来处理图像时，能将之分成不同的两个区域，再使用CCA（连接成分分析），能让我们走的更远，并能标记连接起来的二元区域，而分出来的区域会更加多且细。
另外，通常情况是会同时标记物体的点和背景的点，所以应该对物体使用8邻原则，对背景/孔使用4邻原则。

Geometric Transformations

图像处理中常常用到几何变换（操作），比如将多个图像带入同一参照系中，以便组合或比较，也可用于消除失真和畸变来使像素间距变得均匀，甚至可以用来简化之后的处理过程，如图5.1中，使平面物体的图像与图像内的轴对齐后，能方便后序处理。

Problem Specification and Algorithm

给定一个变形的图像$f(i, j)$和一个校正的图像$f^{\prime}\left(i^{\prime}, j^{\prime}\right)$，我们可以将其坐标之间的几何变换建模为$i=T_{i}\left(i^{\prime}, j^{\prime}\right)$和$j=T_{j}\left(i^{\prime}, j^{\prime}\right)$，值得注意的是，这里的公式让我们在已知校正图像的坐标后，计算出对应的畸变图像的坐标。
在变换图像前，我们必须事先定义变换的方式，比如变换可以是已知的，也可以是通过失真的样本图像和校正的样本图像之间的一对对的对应点来决定的，对于后面一种情况，主要有两种方案来确定对应关系：

• 通过对已知的一个图案（例如图5.2）进行成像，获取失真后的图像，而校正后的图像可以直接从已知图案中获取。
• 获取同一物体的两幅图像，其中一个图像（称为失真图像）将被映射给另一幅图像（称为校正图像），作为参考的框架。

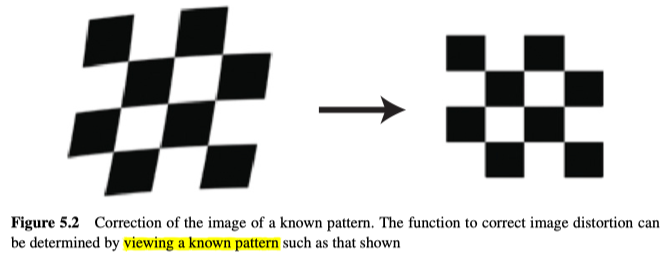
一旦获取了充分的样本失真图像和样本校正图像之间的对应关系，就可以相对简单地计算几何变换函数了，而变换一旦确立，就可以将其应用于失真的图像以及需要相同类型的“校正”的任何其他图像（比如设置固定的相机，其拍摄的所有图像都将具有相同的失真）。
几何变换的应用方式如下：

• 对于输出/校正图像$\left(i^{\prime}, j^{\prime}\right)$的每一点：
  • 使用$T_{i}\left(\right)$和$T_{j}\left(\right)$，来计算它从哪个坐标$(i, j)$变换而来。
  • 根据输入图像中的邻近点，为输出点插值，其中$T_{i}\left(\right)$和$T_{j}\left(\right)$有可能计算出小数，所以坐标有可能在像素点之间。

对于变换，按照一般图像处理的顺序，应该是对于输入图像的每一点，计算其对应输出点的值，但是这样可能会造成输出图像中的部分像素缺失，所以通常的做法是将其反向应用，对每一个输出点，都从输入图像中为其计算一个值。但反向执行计算的唯一缺点是，我们将在变形失真的图像的域内进行插值，而不是在校正后的图像域内。但通常这样做的偏差不大。

Affine Transformations

一般的变换都可使用仿射（Affine）变换来描述：

$$\left[\begin{array}{l} i \\ j \end{array}\right]=\left[\begin{array}{lll} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \end{array}\right]\left[\begin{array}{l} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

仿射变换通常用于简单且常规的变换，例如缩放，旋转等，但也可基于样本的映射（变形和校正图像的点之间的对应关系）来确定未知的变换。

Known Affine Transformations

以下是一些常见的已知变换：

Translation

$$\left[\begin{array}{l} i \\ j \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & m \\ 0 & 1 & n \end{array}\right]\left[\begin{array}{l} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

该方程描述的变换是沿水平轴平移m个单位，沿垂直轴平移n个单位。

Change of Scale (Expand/Shrink)

$$\left[\begin{array}{l} i \\ j \end{array}\right]=\left[\begin{array}{lll} a & 0 & 0 \\ 0 & b & 0 \end{array}\right]\left[\begin{array}{l} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

该方程描述的变换是在水平轴上缩放比例a，在垂直轴上缩放比例b，这么做通常是为了规范图像中的对象的大小。

Rotation

$$\left[\begin{array}{l} i \\ j \end{array}\right]=\left[\begin{array}{ccc} \cos \phi & \sin \phi & 0 \\ -\sin \phi & \cos \phi & 0 \end{array}\right]\left[\begin{array}{l} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

该方程描述的变换是绕原点旋转角度𝜙，它可使图像与轴对齐以便简化后续处理，见图5.3。

Skewing

$$\left[\begin{array}{l} i \\ j \end{array}\right]=\left[\begin{array}{ccc} 1 & \tan \phi & 0 \\ 0 & 1 & 0 \end{array}\right]\left[\begin{array}{l} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

该方程描述的变换是将图像倾斜角度𝜙，能用来消除非线性效果，例如线性扫描相机生成的效果，见图5.3。

Panoramic Distortion

$$\left[\begin{array}{l} i \\ j \end{array}\right]=\left[\begin{array}{lll} a & 0 & 0 \\ 0 & 1 & 0 \end{array}\right]\left[\begin{array}{l} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

全景失真/变形是指图像的宽高比不正确，当镜片（mirror）以不正确的速度旋转时，在线性扫描仪中就会出现，见图5.3。

Unknown Affine Transformations

在很多情况下，要用到的变换是未知的，但是仍然可以使用刚才提到的仿射变换来描述它。然后问题就等效成了求仿射变换中的六个未知参数$a_{00} \ldots a_{12}$。因为是六个未知数，所以我们至少需要三对观测值来确定这些系数，当然观测值越多，得到的变换方程就更精准。具体来说，如果观测到的映射为：$\left(i_{1}, j_{1}\right) \leftrightarrow\left(i_{1}^{\prime}, j_{1}^{\prime}\right)$，$\left(i_{2}, j_{2}\right) \leftrightarrow\left(i_{2}^{\prime}, j_{2}^{\prime}\right)$和$\left(i_{3}, j_{3}\right) \leftrightarrow\left(i_{3}^{\prime}, j_{3}^{\prime}\right)$，则对于：

$$\left[\begin{array}{l} i \\ j \end{array}\right]=\left[\begin{array}{lll} a_{00} & a_{01} & a_{02} \\ a_{10} & a_{11} & a_{12} \end{array}\right]\left[\begin{array}{c} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

我们可以重新排列为：

$$\left[\begin{array}{c} i_{1} \\ j_{1} \\ i_{2} \\ j_{2} \\ i_{3} \\ j_{3} \end{array}\right]=\left[\begin{array}{cccccc} i_{1}^{\prime} & j_{1}^{\prime} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & i_{1}^{\prime} & j_{1}^{\prime} & 1 \\ i_{2}^{\prime} & j_{2}^{\prime} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & i_{2}^{\prime} & j_{2}^{\prime} & 1 \\ i_{3}^{\prime} & j_{3}^{\prime} & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & i_{3}^{\prime} & j_{3}^{\prime} & 1 \end{array}\right]\left[\begin{array}{c} a_{00} \\ a_{01} \\ a_{02} \\ a_{10} \\ a_{11} \\ a_{12} \end{array}\right]$$

将两边都乘以正方矩阵的逆，就能求解系数，如图5.4所示。但是如果有更多的观测值，那么矩阵将不是正方形，我们必须使用伪逆。

Perspective Transformations

大多数摄像机都是通过透视投影来形成图像的，因为3D世界的光线都是通过单个点（小孔成像）或镜头投影到图像平面上。但如果观察的平面与相机的平面不平行时，仅依靠仿射变换，将无法正确校准该平面的试图（如图5.4仿射变换校正的车牌的右下方），所以我们就需要更复杂的变换模型：

$$\left[\begin{array}{c} i \cdot w \\ j \cdot w \\ w \end{array}\right]=\left[\begin{array}{ccc} p_{00} & p_{01} & p_{02} \\ p_{10} & p_{11} & p_{12} \\ p_{20} & p_{21} & 1 \end{array}\right]\left[\begin{array}{c} i^{\prime} \\ j^{\prime} \\ 1 \end{array}\right]$$

对于此变换，我们至少需要四对观测点，可通过以下所示计算出系数：
其中$i \cdot w=p_{00} \cdot i^{\prime}+p_{01} \cdot j^{\prime}+p_{02}$以及$w=p_{20} \cdot i^{\prime}+p_{21} \cdot j^{\prime}+1$
所以$i=p_{00} \cdot i^{\prime}+p_{01} \cdot j^{\prime}+p_{02}-p_{20} \cdot i \cdot i^{\prime}-p_{21} \cdot i \cdot j^{\prime}$
同样的，可得出$j=p_{10} \cdot i^{\prime}+p_{11} \cdot j^{\prime}+p_{12}-p_{20} \cdot j \cdot i^{\prime}-p_{21} \cdot j \cdot j^{\prime}$。

所以使用四对观察之后可得到：

$$\left[\begin{array}{c} i_{1} \\ j_{1} \\ i_{2} \\ j_{2} \\ i_{3} \\ j_{3} \\ i_{4} \\ j_{4} \end{array}\right]=\left[\begin{array}{cccccccc} i_{1}^{\prime} & j_{1}^{\prime} & 1 & 0 & 0 & 0 & -i_{1} i_{1}^{\prime} & -i_{1} j_{1}^{\prime} \\ 0 & 0 & 0 & i_{1}^{\prime} & j_{1}^{\prime} & 1 & -j_{1} i_{1}^{\prime} & -j_{1} j_{1}^{\prime} \\ i_{2}^{\prime} & j_{2}^{\prime} & 1 & 0 & 0 & 0 & -i_{2} i_{2}^{\prime} & -i_{2} j_{2}^{\prime} \\ 0 & 0 & 0 & i_{2}^{\prime} & j_{2}^{\prime} & 1 & -j_{2} i_{2}^{\prime} & -j_{2} j_{2}^{\prime} \\ i_{3}^{\prime} & j_{3}^{\prime} & 1 & 0 & 0 & 0 & -i_{3} i_{3}^{\prime} & -i_{3} j_{3}^{\prime} \\ 0 & 0 & 0 & i_{3}^{\prime} & j_{3}^{\prime} & 1 & -j_{3} i_{3}^{\prime} & -j_{3} j_{3}^{\prime} \\ i_{4}^{\prime} & j_{4}^{\prime} & 1 & 0 & 0 & 0 & -i_{4} i_{4}^{\prime} & -i_{4} j_{4}^{\prime} \\ 0 & 0 & 0 & i_{4}^{\prime} & j_{4}^{\prime} & 1 & -j_{4} i_{4}^{\prime} & -j_{4} j_{4}^{\prime} \end{array}\right]\left[\begin{array}{c} p_{00} \\ p_{01} \\ p_{02} \\ p_{10} \\ p_{11} \\ p_{12} \\ p_{20} \\ p_{21} \end{array}\right]$$

与仿射变换相似，我们也可以通过将两边乘以方矩阵的逆，来确定系数。效果如图5.4和图5.5所示。

Specification of More Complex Transformations

仿射变换和透视变换都是线性变换，都可以通过矩阵来计算，但在某些情况下（例如，将不同时间或用不同设备拍摄的两个医学图像对齐），就需要更复杂的转换。

这些变换通常使用，项目数量预定义的多项式来近似表示：

$$\begin{aligned} i=T_{i}\left(i^{\prime}, j^{\prime}\right)=& a_{00}+a_{10} i^{\prime}+a_{01} j^{\prime}+a_{11} i^{\prime} j^{\prime}+a_{02}\left(j^{\prime}\right)^{2}+a_{20}\left(i^{\prime}\right)^{2}+a_{12} i^{\prime}\left(j^{\prime}\right)^{2}+a_{21}\left(i^{\prime}\right)^{2} j^{\prime} \\ &+a_{22}\left(i^{\prime}\right)^{2}\left(j^{\prime}\right)^{2}+\ldots \\ j=T_{j}\left(i^{\prime}, j^{\prime}\right)=& b_{00}+b_{10} i^{\prime}+b_{01} j^{\prime}+b_{11} i^{\prime} j^{\prime}+b_{02}\left(j^{\prime}\right)^{2}+b_{20}\left(i^{\prime}\right)^{2}+b_{12} i^{\prime}\left(j^{\prime}\right)^{2}+b_{21}\left(i^{\prime}\right)^{2} j^{\prime} \\ &+b_{22}\left(i^{\prime}\right)^{2}\left(j^{\prime}\right)^{2}+\ldots \end{aligned}$$

同样的，为了求解多项式的系数，也需要知道失真和校正图像之间的一些对应关系，其最小数量由多项式的阶数定义（至少是项数的一半），解决方程式中所涉及的数学与前两个相似，而为了准确的计算系数：

• 找到的对应关系的点必须在整个图像上均匀分布；
• 不能包括不正确的对应关系；
• 使用的对应点越多越好；
• 对应关系的点的位置，应该尽量以最高的精度表示；
• 当计算逆矩阵或伪逆矩阵时，必须非常小心地处理矩阵，因为可能会存在数值不稳定的问题（因为大数和小数被组合在一起运算，而其中小数的准确性对于结果至关重要）。

如果几何运算太复杂而无法用多项式近似，可将图像进行分区，然后为每个分区确定一个变换来近似估计图像。

Interpolation

对于变换函数映射出的失真图像中的坐标而言，它不太可能精确地对应于任何一个像素，所以我们需要根据对应坐标附近的像素值来进行插值。插值有很多方案，这里详细介绍三种：

Nearest Neighbour Interpolation

$$f^{\prime}\left(i^{\prime}, j^{\prime}\right)=f(\text { round }(i), \text { round}(j))$$

在最近点插值法中，仅对真实坐标进行四舍五入，取最近的像素点的值。虽然简单，但这种方案会经常导致非常明显的块状效应，如图5.6。特别是对于具有直线边界的对象而言，会更明显，出现像阶梯一样的效果，因此很少使用。

Bilinear Interpolation

$$\begin{aligned} f^{\prime}\left(i^{\prime}, j^{\prime}\right)=&(\operatorname{trunc}(i)+1-i)(\operatorname{trunc}(j)+1-j) f(\operatorname{trunc}(i), \operatorname{trunc}(j)) \\ &+(i-\operatorname{trunc}(i))(\operatorname{trunc}(j)+1-j) f(\operatorname{trunc}(i)+1, \operatorname{trunc}(j)) \\ &+(\operatorname{trunc}(i)+1-i)(j-\operatorname{trunc}(j)) f(\operatorname{trunc}(i), \operatorname{trunc}(j)+1) \\ &+(i-\operatorname{trunc}(i))(j-\operatorname{trunc}(j)) f(\operatorname{trunc}(i)+1, \operatorname{trunc}(j)+1) \end{aligned}$$

该插值方案基于四个最接近的相邻像素$f(t r u n c(i), t r u n c(j)), f(t r u n c(i)+1, t r u n c(j)), f(t r u n c(i), t r u n c(j)+1), f(t r u n c(i)+1, t r u n c(j)+1)$，根据它们与实际点$(i, j)$的距离，加权求和得来，权重与它们到实际点$(i, j)$的绝对距离成比例关系（介于 0.0和1.0），另外该插值方案假定亮度函数是双线性的，所以权重分别取了水平和竖直方向上的距离的乘积，另外，由于离得越近权重越高，所以权重使用了实际点到对称的点的距离的值，以提供与该点的实际距离的反向衡量。
线性插值克服了最邻点插值所引起的块效应，但是会轻微的降低分辨率以及造成模糊，如图5.7所示。

Bi-Cubic Interpolation

双三次插值不仅克服了最近点插值中出现的阶梯状边界问题，也解决了双线性插值的模糊问题。它通过使用双三次多项式曲面上的16个邻近点，来局部估计，改善插值。该函数与拉普拉斯算子（能用于锐化图像）非常相似。
双三次插值经常在栅格显示中使用，这就是为什么图像在显示屏上极具放大后很少会出现块状的原因，如5.8所示。

Modelling and Removing Distortion from Cameras

在照相机系统（即照相机和镜头）中发生的几何变形和校正，是计算机视觉中常见的几何变形和校正形式之一。
针孔相机提供了一个照相机系统的简化模型，但实际上，许多真实的摄像机系统都无法使用该模型进行精确建模，因此还需要对由于物理设置以及镜头引起的失真进行建模。

Camera Distortions

相机系统中经常会出现两种形式的畸变：（i）径向畸变（辐射型变形）和（ii）切向畸变。
Radial distortion，径向畸变是径向（放射状）对称的畸变，其畸变的程度与该点到相机光轴（通常在图像中心附近）的距离有关。这种畸变实际上是由于放大倍数在变化。如果放大倍数随着与光轴的距离的增加而减小，该变形应称为barrel distortion，桶状畸变(广角)。 另一方面，放大倍数反而增加了，则称为pincushion distortion，枕状畸变（长焦）。
如果我们假设图像$f(i, j)$的原点就在光轴上，则：

$$\begin{array}{l} i^{\prime}=i\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right) \\ j^{\prime}=j\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right) \end{array}$$

其中$f^{\prime}\left(i^{\prime}, j^{\prime}\right)$是校正的图像，$r=\sqrt{i^{2}+j^{2}}$是到光轴的距离，$k_{1}, k_{2}, k_{3}$是形容该畸变的参数。

Tangential distortion，切向畸变是当透镜未完全平行于成像平面时会发生的畸变，它会导致放大倍率不均匀，在这种情况下，放大倍率会从成像平面的一侧到另一侧变化，再次假设图像的原点在光轴上，则可以将切向畸变建模为：

$$\begin{array}{l} i^{\prime}=i+\left(2 p_{1} i j+p_{2}\left(r^{2}+2 i^{2}\right)\right) \\ j^{\prime}=j+\left(2 p_{2} i j+p_{1}\left(r^{2}+2 j^{2}\right)\right) \end{array}$$

其中$r=\sqrt{i^{2}+j^{2}}$是到光轴的距离，$p_{1}, p_{2}$是形容该畸变的参数。

Camera Calibration and Removing Distortion

为了确定是哪些参数造成的成像系统的各种畸变，有必要对其进行校准。通常，这意味着同时确定畸变参数和摄像机型号。首先给相机系统展示一个已知的校准对象，如图5.9所示，并不断的变换位置和方向。然后可以使用，与之前从样本点中确定仿射变换和透视变换过程中使用到的，类似的数学方法来提取模型参数。

校准后，只需根据公式将其变形，即可消除该相机拍摄的图像中的任何畸变。

Edges

图像的分割是指将图像分成多个部分的过程，以便分离不同的对象，或将对象的各个部分分离，是理解图像内容（image understanding的目标）中必不可少的步骤之一。解决图像分割主要有两种方法：

1. 边缘处理，即识别图像中的不连续性（边缘）。
2. 区域处理，我们在图像中寻找同质区域（或部分），其中最简单的示例比如二元视觉，当然也有更为复杂的方法。

这些表示可以，也应该是互补的，即边缘能描绘出同质区域。但事实上，很难确定边缘在哪里，因为如果它是可确定的，意味着边缘图像要是唯一的，但是对于大多数图像，没有绝对正确的答案，因为答案通常是主观的，这取决于观察者，也取决于分割的目的，所以基于边缘的视觉的许多技术的目标，都是根据边缘或区域确定场景的最佳表示。

Edge Detection

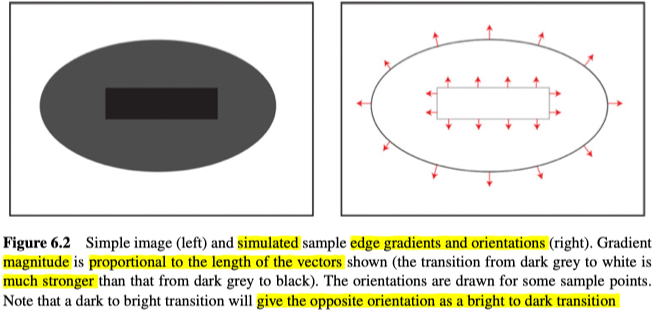
边缘检测通常是针对单个通道（灰度）图像展开的，其中边缘是指亮度突然变化的位置，所以我们通常从2D导数（即变化率）的角度来考虑它。另外，因为图像是处于离散域中，所以尽管亮度变化通常发生在像素之间而不是在具体像素上，我们还是将亮度突然变化的位置视为边缘像素，其中，sobel边缘检测的示例如图6.1所示。

由上图，我们也可以发现，每个边缘像素，既有梯度大小/gradient（变化率），也有方向/orientation（最快增长的方向），如图6.2所示。

通常，要么使用一阶导数运算符，要么使用二阶导数运算符（或者两者的某种组合）来执行边缘检测。一阶导数能得到边缘上的局部最大值（变化率最大的地方），二阶导数能得到边缘上的“跨零点（zero-crossing）”（函数从正无穷到负无穷，或者反过来的地方），如图6.3所示。

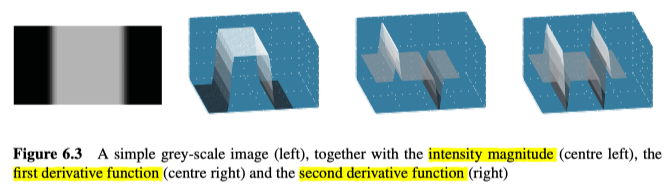
这里值得一提的是，导数是运用在连续的函数的，但是图像是在离散域中处理的，所以为了近似的估计导数（第一、第二），我们使用图像像素之间的差值。

First Derivative Edge Detectors

一阶导数的边缘检测器（其实有很多，本文只介绍几个效果明显的）先计算出两个偏导数，然后再将它们组合起来，以确定每个边缘点的梯度和方向值。最后的梯度结果，必须进行非最大值抑制以及阈值处理。

Roberts Edge Detector

该边缘检测器的两个偏导数考虑了对角线上的像素差异：

$$\begin{array}{l} \delta_{1}(i, j)=f(i, j)-f(i+1, j+1) \\ \delta_{2}(i, j)=f(i+1, j)-f(i, j+1) \end{array}$$

此类函数通常是用与图像卷积的滤波器来表示的，以便在整个图像上计算该函数（将卷积滤波器移至图像中每个可能的位置，与对应的像素进行卷积操作）:

$$\delta_{1}(i, j)=\left[\begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array}\right] \quad \delta_{2}(i, j)=\left[\begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array}\right]$$

而梯度则以两个偏导数的RMS（Root-Mean-Square，均方根）或绝对差之和来计算。至于方向，则使用反正切tan函数计算。

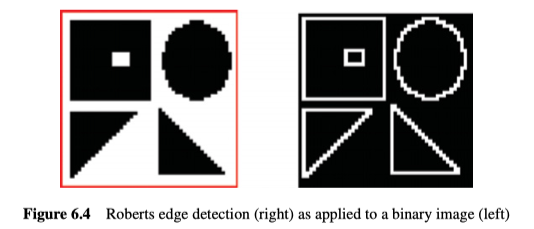
对于二进制图像（图6.4），Roberts算子得到的结果非常好，很干净（其中的点要么是边缘点要么不是），且边缘只有一个像素宽。其实在本文中，Roberts是唯一一个，能用在，也是应该用在二进制图像上的一阶边缘检测器。

对于灰度图像（图6.5），Roberts算子得到的结果似乎很差。主要因为在真实图像中，边缘对应的变化不会突然出现（在两个像素之间突然出现），而是在几个像素上完成变化，而Roberts算子是基于相邻点的。另外也因为图像中的任何噪声都能严重影响其偏导数的计算。
另外，计算出的梯度，只是根据I轴和J轴的二分之一个像素计算而来的，其中的中点位于两个偏导数之间，正由于偏导数的这种相交方式，Roberts运算符通常被称为Roberts cross-operator、Roberts交叉运算符。

Compass Edge Detectors

Compass边缘检测器中，最著名的两个例子是Sobel和Prewitt，它们分别定义了八个偏导数，其中Prewitt定义的八个偏导数为：

$$h_{1}(i, j)=\left[\begin{array}{rrr} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \end{array}\right] \quad h_{2}(i, j)=\left[\begin{array}{rrr} 0 & 1 & 1 \\ -1 & 0 & 1 \\ -1 & -1 & 0 \end{array}\right] \quad h_{3}(i, j)=\left[\begin{array}{ccc} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \end{array}\right]$$ $$h_{4}(i, j)=\left[\begin{array}{rrr} -1 & -1 & 0 \\ -1 & 0 & 1 \\ 0 & 1 & 1 \end{array}\right] \quad h_{5}(i, j)=\left[\begin{array}{rrr} -1 & -1 & -1 \\ 0 & 0 & 0 \\ 1 & 1 & 1 \end{array}\right] \quad h_{6}(i, j)=\left[\begin{array}{rrr} 0 & -1 & -1 \\ 1 & 0 & -1 \\ 1 & 1 & 0 \end{array}\right]$$ $$h_{7}(i, j)=\left[\begin{array}{rrr} 1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1 \end{array}\right] \quad h_{8}(i, j)=\left[\begin{array}{rrr} 1 & 1 & 0 \\ 1 & 0 & -1 \\ 0 & -1 & -1 \end{array}\right]$$

在这8个偏导数中，只有两个正交的偏导数是真正需要的$h_1$和$h_3$。示例见图6.6，其中（b）代表水平偏导数，（c）代表垂直偏导数。另外，由于偏导数可以是正数或负数，所以图中灰色表示0，白色表示最大正值，黑色表示最大负值。

而至于Sobel，对应的偏导数为：

$$h_{1}(i, j)=\left[\begin{array}{rrr} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{array}\right] \quad h_{3}(i, j)=\left[\begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \end{array}\right]$$

分别用于Sobel或Prewitt的两个偏导数，都可用于计算梯度和方向。如图6.7所示，其中（c）是所有点的方向图，（d）是阈值处理的梯度，（e）是边缘点的方法，另外，由于方向是个圆形的方向，其中$0^{\circ}$是黑色，$1^{\circ}$到$359^{\circ}$是白色。

Sobel和Prewitt都在偏导数的卷积mask中，有效地整合了平滑因子，另外，它们也考虑了那些稍微分开的点，这两个因素共同提高了它们在真实的灰度图像上的表现（与Roberts算子的表现相比）。另外这两种算子的偏导数都以特定像素为中心，因此它确定的边缘的位置不会发生偏移（而Roberts算子会导致1/2个像素的偏移）。
Sobel和Prewitt之间的唯一区别，是在偏导数两边的平滑滤波器的权重，所以它们之间的结果差异不大。

Computing Gradient and Orientation

一阶导数的边缘检测器，通过将两个正交的偏导数结合（通常是Root-Mean-Square，也称为$l^{2}$ -norm、$l^{2}$ 范数），来计算边缘的梯度：

$$\nabla f(i, j)=\sqrt{\left(\frac{\delta f(i, j)}{\delta i}\right)^{2}+\left(\frac{\delta f(i, j)}{\delta j}\right)^{2}}$$

出于速度原因，有时使用偏导数的绝对值之和来近似估算：

$$\nabla f(i, j)=\left|\frac{\delta f(i, j)}{\delta i}\right|+\left|\frac{\delta f(i, j)}{\delta j}\right|$$

至于边缘点的方向，则使用带有两个参数的反正切函数计算出（以区分所有360度）：

$$\phi(i, j)=\arctan \left(\frac{\delta f(i, j)}{\delta j}, \frac{\delta f(i, j)}{\delta i}\right)$$

在计算机中应使用atan2，对编程更方便。

Edge Image Thresholding

边缘图像的阈值化是应用于梯度图像的二元阈值操作。但事实上，边缘有几个像素宽，且这些像素通常都会导致梯度响应，因此阈值处理后，在边缘也会产生多个响应，如图6.8所示。

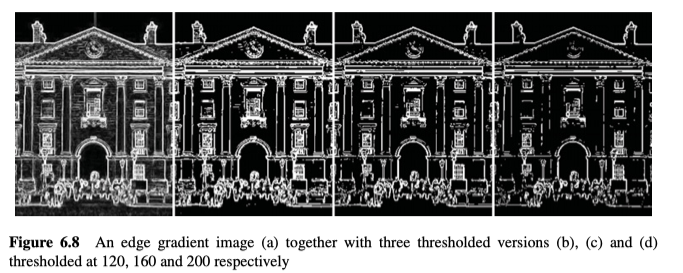
因此，我们需要在对其阈值处理之前，添加一个额外的阶段，在该阶段中，中心最大值以外的所有梯度响应（对于任何给定的边缘点）都将被抑制，也就是non-maxima suppression、非最大值抑制。

Non-maxima Suppression

首先是要确定哪些边缘点是中心点（即沿边缘轮廓上的每个点的主要响应），该算法是通过梯度大小和方向信息来判断的。通过当前点的方向，它能知道当前点的两边是哪些点，如果该点的梯度小于任何一边的梯度，则抑制该点，示例见图6.9，详细介绍见图6.10。

具体算法：

• 量化边缘方向（将所有方向分类为八个方向，因为仅考虑八个边界点）
• 对所有的点$(i, j)$
  • 寻找与边正交（垂直）的两个点
  • 如果gradient$(i, j)$<这两点的任何一个梯度
    • output $(i, j)=0$
    • 否则output $(i, j)=\operatorname{gradient}(i, j)$

Second Derivative Edge Detectors

二阶导数的边缘检测器，得到的是变化率的变化率，但实际上也是使用单个卷积滤波器在图像的离散域中进行卷积计算。其中最常见的二阶导数滤波器之一是拉普拉斯算子，它的两个离散估计分别为：

$$h(i, j)=\left[\begin{array}{rrr} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{array}\right]$$

或者:

$$h(i, j)=\left[\begin{array}{rrr} 2 & -1 & 2 \\ -1 & -4 & -1 \\ 2 & -1 & 2 \end{array}\right]$$

值得注意的是，这些估计给了中心像素很大的权重，所以如果存在噪声时会出现问题。因此，通常在拉普拉斯滤波之前，先进行某种类型的平滑处理。
二阶导数边缘检测器可以用于确定梯度的大小和位置，但是它不能用于确定梯度的方向。而且就算是梯度大小，也需要知道在zero crossing处的二阶导数函数的斜率，这有点复杂，因此经常使用一阶导数函数来求梯度大小。那二阶导数边缘算子还有什么用途呢，实际上它的目的是高精度的确定边缘位置。如接下来所展示的两种算子。

Laplacian of Gaussian

高斯拉普拉斯算子现在仍是使用最广泛的检测器之一。如前所述，二阶导数的边缘检测器易受噪声影响，因此需要在它之前通过平滑处理来降低噪声水平。 平滑滤波器必须满足两个条件：（i）它是平滑的，并且在频域中受频带限制（即它必须限制图像中边缘出现的频率）；（ii）它表现出良好的空间定位性（即平滑滤波器禁止移动任何边缘，或更改它们之间的空间关系）。 解决此问题的最佳方法是使用高斯平滑，其中$\sigma^{2}$表示高斯函数的宽度：

$$G(i, j)=e^{-\frac{i^{2}+j^{2}}{2 \sigma^{2}}}$$

为了计算二阶导数，应首先将高斯平滑算子应用于图像，然后再应用拉普拉斯算子，如图6.11所示。但是，可以将这两个运算符组合在一起，并将它们作为单个“高斯拉普拉斯算子”同时应用于图像。此运算符的卷积过滤器定义如下：

$$h(i, j)=\frac{1}{\pi \sigma^{4}}\left(\frac{i^{2}+j^{2}}{2 \sigma^{2}}-1\right) e^{-\frac{i^{2}+j^{2}}{2 \sigma^{2}}}$$

该卷积mask的形状，在中心为正，而在附近为负，再远一点逐渐变为零。所以它也常常被称为墨西哥帽过滤器，见图6.12所示。

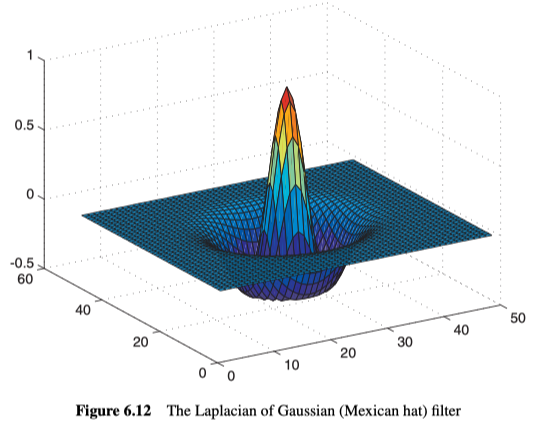
与普通边缘算子相比，该算子可以考虑更大的面积，但这并不总是件好事，因为并不知道该区域中是否存在许多边缘。此外，有时过多进行的平滑处理，会丢失诸如拐角之类的精细细节。另外，该算子给出了保证的边缘闭环（guaranteed closed loops of edges），这个优点很重要，但对某些应用程序（或某些类型的后处理）会造成问题。另外，神经生理学实验已经表明，人类的视觉系统（以神经节细胞的形式）执行的操作与Laplacian of Gaussian十分相似。
为了在实践中使用该滤波器，需要提出一种有效的应用方法，因为滤镜的mask通常很大（取决于$\sigma$的值），所以可以将二维的Laplacian of Gaussian函数分成四个一维的卷积操作，这样能计算的更快。另外，Laplacian of Gaussian通常用高斯的差（两个用不同的$\sigma$值平滑处理后的图像之间的差）来近似估计。
在二阶导数图像中找到zero crossings并不简单。我们不能只寻找零（因为域并不连续）。不过，如果一个点的符号（+ ve或–ve）与该行上的上一个点，或者该列中的上一个点的符号不同，将可以将它们标记为zero crossing。但是如果这样做，我们将舍弃二阶导数的主要优势之一（即，可以高精度的确定边缘位置）。

Multiple Scales

许多图像处理技术要么使用局部的单个像素，要么使用一个局部区域中的频繁像素。但一个主要问题，是要知道使用多大的邻域，以及“正确”的领域大小取决于所调查对象的大小。这实际上是图像内的尺度问题。知道对象/物体是什么，就可以清楚地理解应该如何解释图像，这对于工业应用是可以接受的，因为工业要求固定，物体已知，但对于一般的视觉而言似乎是棘手的（鸡和鸡蛋类型的问题）。所以一种解决方案是同时研究不同分辨率（比例）下的图像。通过创建具有多种分辨率的模型，然后研究模型在不同分辨率下改变的方式，以获得在一个尺度上无法获取的元知识。
回到Laplacian of Gaussian，David Marr（Marr，1982）提出了一种可能性，即，应该使用不同的高斯算子对图像进行平滑处理，然后，跨多个尺度的对应关系可以被用来识别明显的不连续性（即，zero crossings）。有关在两个尺度下处理的图像的示例，见图6.13。

Canny Edge Detection

Canny边缘检测器将一阶导数和二阶导数的边缘检测相结合，以计算边缘梯度和方向，它旨在优化以下三个标准：

1. Detection - 边不能被遗漏。
2. Localisation - 实际的边缘和确定的边缘之间的距离应最小化。
3. One response - 对单个边的多个响应应最小化。

具体算法：

1. 以标准偏差𝜎，来用高斯进行卷积增加模糊，去噪声。
2. 使用高斯卷积后的图像的一阶导数，去估算边的法向量方向（即orientation）。
3. 找到边，抑制non-maxima值。首先在高斯卷积图像的二阶导数中搜索zero-crossings得到准确的边缘信息，再通过上一步中计算出的边缘方向来抑制非最大值。
4. 边的梯度是根据高斯卷积图像的一阶导数计算的。
5. 利用hysteresis、磁滞现象来对边缘进行阈值处理。这里的设想是边缘点是存在于连接着的点的轮廓中的。那么使用两个阈值 – 高梯度阈值（在该阈值上所有点都明确地分类为边缘点）以及低阈值，在该阈值下且与确定为边缘点的点连接的点，也分类为边缘点。这样能解决那些，由于阈值太简单，而将边缘轮廓分裂成多个未连接的片段的问题。
6. 与Marr的探测器类似，我们也可以针对多个尺度（使用不同的高斯）来处理，然后使用“feature synthesis、特征合成”来将不同尺度下的边组合到一起。

Canny检测的边缘图如图6.14所示。

Multispectral Edge Detection

在彩色图像中进行边缘检测并不像看起来那样简单。如果将图像转换为灰度，然后应用边缘检测，某些边缘（两种不同的相邻颜色，但灰度相似）有可能不能被检测出来，如图6.15。

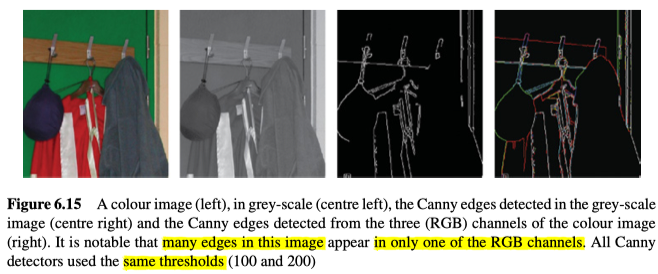
可以发现，从灰度图像导出的边缘图像中，一些很明显的边缘消失了，但是并不是大多数图像都会这样，因此，大部分研究还是仅使用灰度图像进行边缘检测，但是彩色边缘检测还是可以通过多种方式进行：

1. 向量方法。在这些方法中，颜色被视为向量或者一个整体。先计算出Median、中位向量以及向量之间的距离，并将它们用于测量梯度（和方向）。从效果上来看，每种颜色都被视为一个单独的整体（而不是三个单独的维度）。
2. 多维渐变方法。通常使用相对复杂的公式，基于所有通道的数据来计算梯度和方向。
3. 输出融合方法。分别为所有通道单独计算梯度和方向，然后通常使用加权和或最大值法，将其组合为单个结果。

值得注意的是，对色彩空间的选择将对颜色图像的边检测有很大的影响。

Image Sharpening

简单地从原始图像中减去二阶导数的一部分（例如3/10），就能够锐化图像。这具有将边缘加长的效果，见图6.16，示例见图6.17。

Contour Segmentation

对于大多数应用来说，仅提取边缘图像是不够的，我们还需要提取其中包含的信息，并更加明确地表示它，这样能更轻松地进行推理。而边缘信息的提取过程包括，首先确定哪些点是边缘（因为大多数点具有非零梯度），一般通过边缘图像阈值化和非最大值抑制（或通过使用Canny）来实现。然后从图像域中提取边缘数据（例如，使用graph searching、图形搜索，边border refining、边界细化等），并将其以某种方式表示（例如，BCC，图形，直线段的序列和其他几何表示）。
从未封闭的轮廓以及带有T型交界处或十字型交界处的轮廓中，很难提取出一致的表示结果。

Basic Representations of Edge Data

要在图像域外部表示边缘图像数据，有很多种方法，比如：

Boundary Chain Codes

边界链码（BCC）包括一个起点和一个连接到其它点的方向列表，也就是一串点，如图6.18所示。

起始点由（行，列）对指定，然后到下一个点的方向被简化为0到7之间的值（即到相邻像素的八个方向），如图6.19所示。

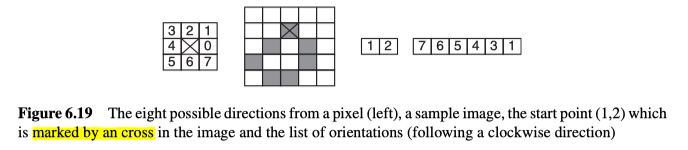
如果将其视为一个形状的表示，那我们还必须考虑它对后续处理（例如形状/物体识别）有多大用处。BCC依赖于orientation、方向，所以如果对象/区域的方向发生变化，相应的表示也将发生很大变化。另外，其表示也会随着对象尺寸的变化而变化，而且它的位置只取决于起始位置，而如果是封闭轮廓，起点在一定程度上可以是任意位置。
另外，可以对边界进行平滑处理以减少噪声，但要谨慎进行以防止形状变形。

Directed Graphs

有向图是由节点（也就是边上的像素）和有向弧线（边界像素/节点之间的连接）组成的结构，见图6.20所示。

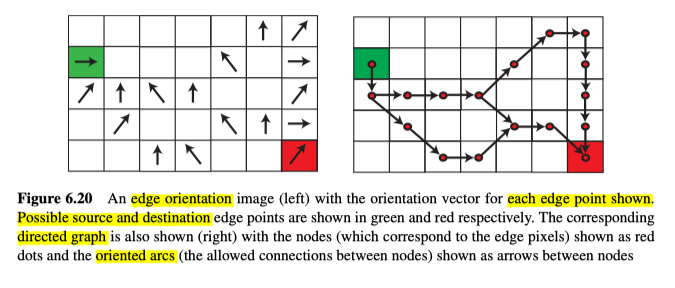
如果边缘像素的梯度值$s\left(x_{\mathrm{i}}\right)$大于某个阈值（$T$），则将其作为节点添加到图表中。之后，为了确定哪些节点通过弧线连接在一起，我们查看每个节点$n_i$的方向$s\left(x_{i}\right)$，来确定哪些相邻像素$x_j$可以被连接。如图6.20a所示，方向向量与边缘轮廓垂直，因此最有可能的下一个像素将位于该点的侧面（因此可能是一个弧形）。同样的，该像素两侧的像素（即$\pm 45^{\circ}$）也能通过弧线连接。如果这些像素中的任何一个具有关联的节点$n_j$，且两个相应像素之间的方向差小于$\pi / 2$，则添加一个从$n_i$到$n_j$的有向弧，具体算法如下：

给定一个边缘图像，其中每个像素$x_i$都有一个梯度$s\left(x_{i}\right)$和一个方向$\mathbf{s}\left(x_{i}\right)$
对于每一个像素$x_i$：
如果梯度$s\left(x_{i}\right)$比阈值T大：
创建一个对应的节点$n_i$
对于每一个节点$n_i$：
对于每一个邻节点$n_j$：
如果$x_j$是相对于$x_i$的$\left[s\left(x_{i}\right)-3 \pi / 4, s\left(x_{i}\right)-\pi / 2, s\left(x_{i}\right)-\pi / 4\right]$的其中的一个方向并 且$\left(\left|\mathrm{s}\left(x_{\mathrm{i}}\right)-\mathrm{s}\left(x_{\mathrm{j}}\right)\right|<\pi / 2\right)$
创建一个有向弧来连接$n_i$和$n_j$

该算法似乎是合理的，但是如图6.20b的图形的右侧对角线向上倾斜的弧线所示，就会发现，当考虑下个节点允许的方向时，还应该考虑边缘像素的相对位置。

Border Detection

边界检测可以看做是搜索源和目的地之间的最佳路径，也可以是搜索图像中的所有边缘点的最佳表示。在第一种情况下，所解决的问题需要有很多先验知识，比如至少源和目的地要事先知道，第二种情况下，通常会尝试提取场景中的所有边缘轮廓的一般表示，以进行进一步处理。

A-algorithm Graph Search (for the Optimal Path)

创建了有向图（请参见第6.2.1.2节）之后，现在需要在图内搜索从源节点到目标节点的最佳路径，算法如下：

给定一个源节点$n_A$以及一个目标节点$n_B$以及一个包含它们的图结构：
将$n_A$放入open节点中（OPEN），并设置累积损失cost $f\left(n_{\mathrm{A}}\right)=0$
当$\left((\mathrm{OPEN} \neq \emptyset) \mathrm{AND}\left(n_{\mathrm{B}} \notin \mathrm{OPEN}\right)\right)$时：
选择OPEN中损失$f\left(n_{\mathrm{y}}\right)$最低的节点$n_y$
将$n_y$从OPEN中移走，并将其所有后节点以及累积损失放入OPEN中
如果 $n_B$ 属于OPEN
最佳路径已找到
否则 没有可用路径

但此算法也会遇到问题，比如遇到闭环容易陷入无限循环，不过可以通过给进入过OPEN的节点打标记，这样就不会再次进入OPEN。另外一个问题就是，它拓展节点时，没有考虑目的地节点在哪里，因此考虑了所有方向，有点浪费资源，因此可以考虑使用“Gradient Field Transform”，来对OPEN列表里面的所有节点都同时考虑累积损失和到目的地的损失。

Cost Function

对于A algorithm或Gradient Field Transform，都需要能够确定OPEN列表中节点的成本（也就是要确定，从源节点到OPEN列表中每个节点的路径成本，以及从OPEN列表中每个节点到目标节点的路径成本），可选的范围有限：

1. 边缘的强度（即梯度）。在OPEN列表中，将节点$n_i$添加进路径的成本为$\left(\operatorname{Max}_{\text {imare }} s\left(x_{k}\right)\right)-s\left(x_{i}\right)$。在这种情况下，添加梯度最强的边缘点将不会增加成本，而添加梯度较小的边缘点会增加更多的成本。这种方法似乎是合理的，并且经常能给出良好的结果，但是也应该考虑它的意义，因为图像中的所有边缘点都与阈值进行了比较，这种对梯度的考虑是已经包含在图表中了，所以意义不大。
2. 边界曲率。其对应成本为$\left|s\left(x_{i}\right)-s\left(x_{j}\right)\right|$。此函数会对方向上的变化进行惩罚，这似乎是合理的。但是，如果能通过像素的相对位置（和方向）来对连续性进行度量，并将成本定义为连续性的倒数，可能会更好。
3. 到估计（预期）边界的距离。如果能求得一个近似的边界，这将是一种有用的成本度量方法，而近似边界可以通过先验图像中获取，也可以从先前处理的较低分辨率图像中获取（在许多应用程序中都这样做的，以便降低计算成本） ）。
4. 到目的地的距离。在没有近似边界的情况下，估计到目的点的成本的唯一实用方法，是测量从每个节点到目标节点的欧几里得距离。

More Efficient Search

下面是一些提高图表搜索效率的一些方法：

1. 多分辨率处理。先在较低分辨率图像中，估计近似的边界。这个方法假定，可以在较低分辨率的图像中检测到边界。
2. 深度优先搜索。通过将所有扩展节点的成本减少为最佳后继节点的成本（其成本将为0—因此来保证此节点将立即再次被扩展）来降低在不良的边缘上扩展的可能性。
3. 纳入更高阶的知识。比如，到预期边界的距离。
4. 修剪结果树。删除每单位长度成本过高的路径。
5. 最高成本。确定路径的最大开销，因此一旦OPEN列表中的最小开销大于该最大值，便停止搜索。

Heuristic Search for All Image Borders

该算法的目的是以最好的方式，表示图像中的所有边缘点。
该技术尝试提取可以使用BCC表示的边缘点链。它通过反复从最强的未使用的边缘点开始，向前建立一个边缘点链（如果没形成循环），则再向后建立边缘点链，直到用完所有边缘点，如图6.21所示，它使用与之前创建过程中所使用的相似的规则，若存在多个边缘点，则应该选择最相似或最连续的边缘点。
而后处理阶段的一个基本处理是，清理生成的轮廓，获取薄的边缘，消除照明变化并填充小间隙（有时使用更复杂的系统来填充缺口）。

具体算法如下：

给定一个边缘图像，其已经抑制了非最大值，以及进行了半阈值化：
当图像中有未使用的边缘点时
搜寻图像中最强的边缘点
拓展特定边缘点之前的边
拓展特定边缘点之后的边
如果边缘点链长于三个像素，将之储存
根据以下三个准则微调边缘链：
移走任何与更大的边平行的链
移走所有有多重平行边的链
连接任何彼此共线但被单个像素点间隔的链

Extracting Line Segment Representations of Edge Contours

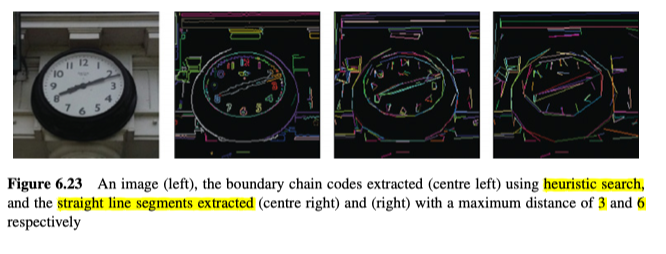
通常，特别是对于人造物体，我们使用直线段来表示边缘轮廓。这些片段汇总了大量的边缘图像数据（取决于它们有多长），因为可以仅由片段的起点和终点的位置表示它们。
但是，图像中的轮廓很少会完美地笔直，因此在提取边缘直线段时，有必要为轮廓线和近似轮廓直线段之间设置一个最大距离容忍值（$t$）, 见图6.22和图6.23所示。

两种常用解决方法如下：

Recursive Boundary Splitting

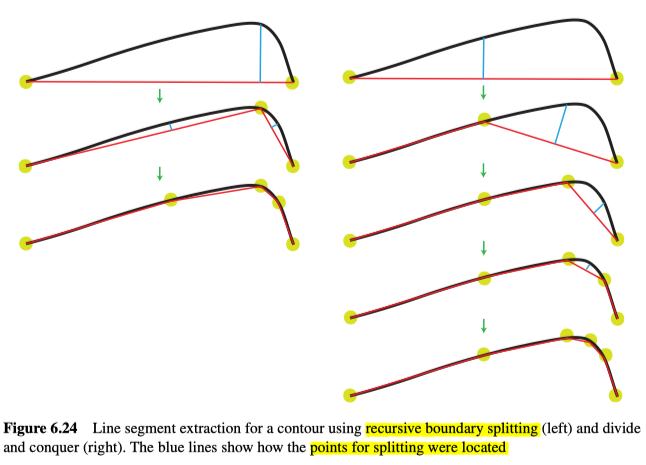
递归边界分割使用数据来将一个轮廓分割为多个部分，以获得分割的位置。
给定边缘轮廓，用一条直线段（从轮廓的起点到终点）对其进行模拟。在距离直线段最远的边缘轮廓上的点，将线段一分为二。不断执行此操作，直到所有直线段距离轮廓的最远距离，都没有超出预设的容忍值为止，见图6.24所示，容忍值不同的两个示例，见图6.23（c）和（d）。

Divide and Conquer

分而治之考虑相同的容忍值，如果轮廓距离直线段太远，则将该线段从中间分开。选择用于分割线段的轮廓点$\left(v_{\mathrm{n}}\right)$，是当前线段$\left(v_{1}, v_{2}\right)$的中垂线上，距离线段最远的轮廓上的点，将其作为一个新的顶点，分出了两个线段$\left(v_{1}, v_{n}\right)$和$\left(v_{n}, v_{2}\right)$，直到所有线段都在容忍值内为止，见图6.24右侧所示。

Comparison

Recursive Boundary Splitting虽然计算成本略大，但是能试着创建更好的表示数据的线段。
对于如图6.24所示的曲线，由于其起点和终点都在边缘轮廓上，因此这两种技术的直线段都位于边缘数据的一侧。这显然并不是对边缘数据的最佳近似估计。

Curved Segments

使用曲线自然能比直线更好地描述了一些物体。但是，曲线的使用提出了一个紧迫的问题。我们应该使用什么样的曲线？是使用曲率恒定的曲线，二阶多项式（圆形，椭圆形，抛物线形）等等？以及，一条曲线在哪里结束，下一条曲线在哪里开始？也很有可能有多种解释，但它们全部同等有效。因此，直线线段还是最常使用的表示。
另外，在处理曲线时，很重要的问题是如何计算轮廓（边缘点）的曲率。通常，我们不能依赖方向值（即，仅计算点到点的方向变化率）。我们甚至不能基于像素在轮廓上的两个最近邻居。相反，要计算沿轮廓线的点$x$处的曲率，我们考虑的是轮廓上在x之前的第n个点，和在x之后的第n个点，然后通过这三个点计算曲率，如图6.25所示。

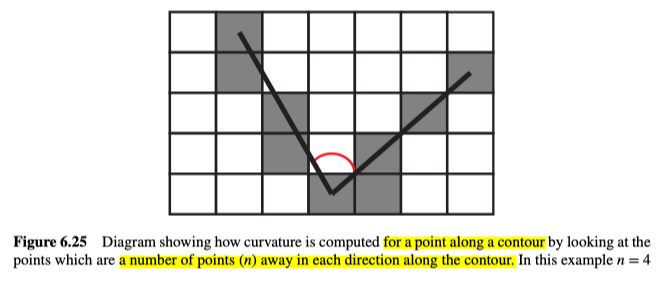
因此，当我们接近“拐角”时，将获得一个增加的值，而在拐角之后，将获得一个减小的值，所以通过在轮廓上寻找局部最大的曲率值时，可以找到沿该轮廓的重要特征点。

Hough Transform

霍夫变换（Illingworth＆Kittler，1988）是一种非常优雅的变换，能直接从图像空间映射到某些特征（例如线，圆或特定形状）存在的概率，如图6.26所示。

霍夫变换能够检测物体的局部。在这些情况下，与一个完整的物体相比，所需的依据的量减少了。
霍夫变换最大的问题就是它的速度太慢了，成本很高，而减少计算成本的方法，例如，如果能有可靠的边缘方向信息并且边缘平滑，则可以使用边缘方向来限制霍夫空间。此外，也可以从较小的分辨率开始处理，在找到代表目标形状的局部最大值之后，生成新的更高分辨率的霍夫空间以获取更高分辨率的局部最大值，最后获得形状的位置 。

Hough for Lines

对于直线，最常用的方程是$j=m i+c$（通常表示为$j=m x+c$），其中m表示直线的斜率，但是该直线方程不能表示某些直线，比如$i=p$，其中p是常数因此需要使用另一种形式的直线方程：

$$s=i . \cos (\theta)+j . \sin (\theta)$$

其中s是直线到原点的正交距离，而$\theta$是该直线和I轴之间的角度。
为了在图像空间中找到线，我们首先将图像空间转换为霍夫空间，其中，坐标轴将为$s$和$\theta$。之后，对于场景的二元边缘图像中的每个边缘点，我们首先确定每一条穿过该点的直线，并将这些直线在霍夫空间中对应的每个cell增加1，而霍夫变换是基于投票性质的检测算法，通过阈值处理，高于阈值的cell，将视为检测到了对应形状，示例如图6.27所示。

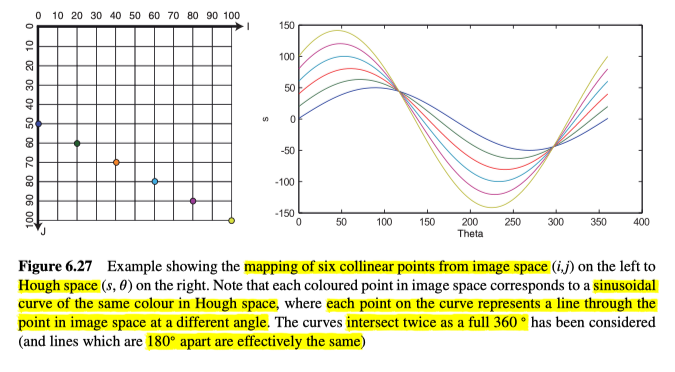
算法如下所示:

• 将霍夫空间累加器中的每个cells$(s, \theta)$初始化为0
• 对于图像空间$(i, j)$中的每个边缘点
  • 根据每一个经过该点的直线，通过使用$s=i . \cos (\theta)+j . \sin (\theta)$，将每个直线映射到霍夫空间中的cells增加1，由于$i$和$j$是已知的，所以只需要对每个可能的$\theta$计算一个s值，即可得到霍夫空间中对应的cells。
• 搜索霍夫空间累加器中的局部最大值，这意味着识别累加器中任何值等于或大于周围cells的cells$(s, \theta)$。

如果要对所有360度进行计算，每条线将被表示两次。
行的行距空间实际上代表每行两次，但是会很方便，因为它可以区分出黑到白的线与白到黑的线，但是在许多应用中，这是不必要的，因此，仅考虑霍夫空间上的前180°，如图6.28所示。

若仅考虑180°，所需的计算操作数就减少了一半。但是，在寻找最大值时更需要小心，因为霍夫空间的另一半将覆盖在它自己身上。
s的最大值和最小值由图像大小定义，但是若将图像上的原点移动到图像中心，其范围将减小。另外，$s$和$\theta$的精度取决于应用程序，但是精度越高，算法就越慢。

Hough for Circles

圆的方程为$(i-a)^{2}+(j-b)^{2}=r^{2}$，其中，$r$是圆的半径，而$(a，b)$是圆的中心。如果我们假设半径为常数，那么只需要确定圆心（a，b），就能指定一个圆。然后使用霍夫变换，就能从图像空间$(i，j)$变换为霍夫空间$(a，b)$，来表示指定的圆存在的可能性，如图6.29所示，其算法与上一节类似，只是方程和霍夫空间的参数不同。

由于霍夫变换能够检测对象的部分，因此“霍夫圆”可以检测中心在图像空间外部的圆。从理论上讲，这样的圆可以达到图像空间外面，半径$r$长的地方，因此，霍夫空间的长和宽实际上应该比图像空间大$2*r$。
另外，由于我们使用了圆上的所有点作为依据，因此可以以更高的精度（即sub-pixel、子像素精度）来检测圆心。同样，这意味着霍夫空间的分辨率将会提高（以表示像素之间的点）。
霍夫圆的一个主要问题是，如果圆的大小事先并不知道，我们就需要一个3D的累加器（第三维表示半径），这为计算量又增加了一个数量级。

Generalised Hough

实际上，霍夫变换可以用来定位任何形状（即使不能用简单的参数方程式来表示该形状）。但是，我们需要在训练阶段学习该形状（必须事先提供形状样本），并将形状存储为R-table的形式。在识别阶段，就可以使用R表在其他图像中搜索该形状。这适用于任何形状，甚至不需要该形状的边缘点是彼此连接的。
首先需要定义一个任意参考点$X^{R}$，参考点可以在任何地方（无论是形状内还是形状外），但一般使用形状中心作为参考，而形状就是根据这个参考点定义的，如图6.30所示。

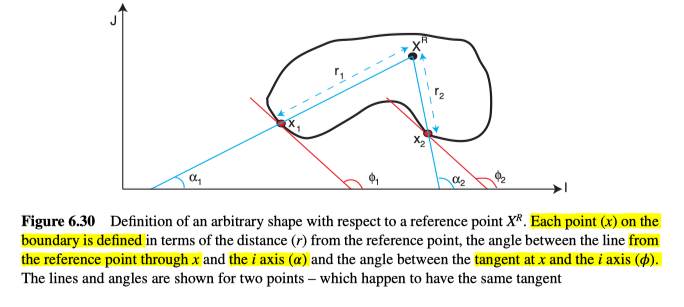
在这之后，形状上的每一个边缘点，都能通过它相对于参考点的位置来表示，表示的信息就储存在R-table中。R-table包括一组指针，每一个都代表一个可能的边方向$\phi$，而每一个指针都指向一个$(r, \alpha)$对的链表，其中$r$是从参考点到边缘点的距离，而$\alpha$是边缘点和参考点之间的线的角度。其中边缘方向已经被量化为多个离散的可能方向。比如图6.32中，方向已经量化为4 bits（16种可能性）。

训练阶段的算法：

• 对于每一个边缘点$x$
  • 确定边缘点$x$与参考点$X^{R}$的距离$r$。
  • 确定边缘点$x$的方向$\phi$（即，切线的方向）。另外，多个点可以具有相同的方向，如图表所示。
  • 确定从参考点$X^{R}$到边缘点$x$的直线的方向$\alpha$。
  • 将$(r, \alpha)$对，添加到R-table中，方向$\phi$的链表中。

为了识别R-table中定义的形状，我们根据形状相对于参考点在霍夫空间的可能性，来累积依据，如下所示：
识别阶段的算法：

• 根据参考点$X^{R}$的坐标，建立累加器，并将所有cells初始化为0。
• 对于每个边缘点：
  • 确定它的边缘方向$\phi$
  • 从R-table中选择合适的$(r, \alpha)$对的链表
  • 对于每一个$(r, \alpha)$对
    • 根据当前边缘点的位置以及$r$和$\alpha$，确定$X^{R}$的位置。并增加在霍夫空间（累加器）中相应的单元格。
• 在霍夫空间（累加器）中寻找局部最大值来寻找形状。

在识别阶段，我们假设大小和边缘方向是固定的，所有霍夫空间中初始化了一个简单的2D累加器，如果允许形状的大小和方向变化，就需要4D的累加器了。

Features

给定一个边缘图像，通常很难从图像序列中确定边缘从一帧到下一帧的局部运动，这可能源于各种各样的原因，比如匹配的不确定性等。如图7.1所示，红色的物体可能扩大，或者朝各种方向移动，更复杂的，三维物体还会旋转、平移、消失。
为了克服这个问题，计算机视觉中的一种常见方法是，利用角(corners)，图像特征(image features)或兴趣点(interest points)。其中，角是两个边缘的交点，而兴趣点则是其中的任何能被稳定定位的点。类似的对特征的使用，大大减少了逐帧之间需要考虑的点，并且每一个点，都比边缘点更复杂。这两个因素都使我们更容易的在帧之间建立可靠的对应关系，如图7.2所示。虽然，角/特征检测通常不是可重复的，也不是很强大，因为拐角的位置可能在帧与帧之间变化很大，也可能消失，同时出现新的角。

大多数的角检测算法，都有一个类似的严谨步骤：

1. 确定角度值。对于图像中的每个像素，基于其局部像素计算角度值。该部分是大多数角检测器的区别所在，而其输出是一个角度图(cornerness map)。
2. 非最大值抑制。如果角度值小于相邻像素，则受到抑制（在n个像素距离内，比如3），以免对同一角产生多个响应。
3. 对角度图进行阈值处理。最后，我们需要选择那些显著的角度值（即，角度值必须高于某个阈值T才能被视为角）。

Moravec Corner Detection

Moravec角检测器，通过比较局部图像块，并计算它们之间的非归一化局部自相关性，来获取一个点周围的局部变化情况，进而判断。具体来说，对于每个像素，它将以该像素为中心的图像块，与其它八个稍微偏移的图像块进行比较（通常在八个方向上各自平移一个像素）。比较的方式，则使用如下的平方差和公式：

$$V_{u, v}(i, j)=\sum_{\forall a, b \in \text {Window}}(f(i+u+a, j+v+b)-f(i+a, j+b))^{2}$$

其中$(\mathrm{u}, \mathrm{v}) \in\{(-1,-1),(-1,0),(-1,1),(0,-1),(0,1),(1,-1),(1,0),(1,1,)\}$，而且窗口大小通常为3×3，5×5或7×7，最后将八个值中的最小值作为角度值，二元解析图如图7.4所示。

实例如图7.5所示。

但它有两个缺陷，进而促使了不同检测器的发展：

1. 各向异性的响应。如图7.5所示，它对对角线的响应非常强烈，但是对竖直线和水平线的响应没那么强烈，所以该操作不是各向同性的。不过可以通过进行平滑的预处理，来降低各向异性。
2. 响应有噪声。Moravec检测器对噪声也很敏感。不过可以通过使用更大的检测区域，或者在应用角检测器之前，先进行平滑处理来减少对噪声的响应。

Harris Corner Detection

Harris角检测器与Moravec角检测器的区别，在于其确定角度值的方式。它使用偏导数而不是平方差和：高斯加权函数，及其矩阵表示的特征值。
对一个图像块$W$进行微小移动（$\Delta i, \Delta j$）后的强度变化为：

$$\operatorname{SSD}_{W}(\Delta i, \Delta j)=\sum_{(i, j) \in W}(f(i, j)-f(i-\Delta i, j-\Delta j))^{2}$$

其二项估计为：

$$f(i-\Delta i, j-\Delta j) \approx f(i, j)+\left[\frac{\delta f(i, j)}{\delta i} \quad \frac{\delta f(i, j)}{\delta j}\right]\left[\begin{array}{l} \Delta i \\ \Delta j \end{array}\right]$$

因此，等式可以写为

$$\begin{aligned} &\operatorname{SSD}_{W}(\Delta i, \Delta j)=\sum_{(i, j) \in W}\left(f(i, j)-f(i, j)-\left[\frac{\delta f(i, j)}{\delta i} \quad \frac{\delta f(i, j)}{\delta j}\right]\left[\begin{array}{l} \Delta i \\ \Delta j \end{array}\right]\right)^{2}\\ &\operatorname{SSD}_{W}(\Delta i, \Delta j)=\sum_{(i, j) \in W}\left(\left[\begin{array}{cc} \frac{\delta f(i, j)}{\delta i} & \frac{\delta f(i, j)}{\delta j} \end{array}\right]\left[\begin{array}{l} \Delta i \\ \Delta j \end{array}\right]\right)^{2}\\ &S S D_{W}(\Delta i, \Delta j)=\sum_{(i, j) \in W}\left(\left[\begin{array}{cc} \Delta i & \Delta j \end{array}\right]\left(\left[\begin{array}{c} \frac{\delta f(i, j)}{\delta i} \\ \frac{\delta f(i, j)}{\delta j} \end{array}\right]\left[\begin{array}{cc} \frac{\delta f(i, j)}{\delta i} & \frac{\delta f(i, j)}{\delta j} \end{array}\right]\right)\left[\begin{array}{l} \Delta i \\ \Delta j \end{array}\right]\right)\\ &\operatorname{SSD}_{W}(\Delta i, \Delta j)=\left[\begin{array}{cc} \Delta i & \Delta j \end{array}\right]\left(\sum_{(i, j) \in W}\left[\begin{array}{c} \frac{\delta f(i, j)}{\delta i} \\ \frac{\delta f(i, j)}{\delta j} \end{array}\right]\left[\begin{array}{cc} \frac{\delta f(i, j)}{\delta i} & \frac{\delta f(i, j)}{\delta j} \end{array}\right]\left[\begin{array}{l} \Delta i \\ \Delta j \end{array}\right]\right.\\ &\operatorname{SSD}_{W}(\Delta i, \Delta j)=\left[\begin{array}{cc} \Delta i & \Delta j \end{array}\right]\left[\begin{array}{cc} \sum_{(i, j) \in W}\left(\frac{\delta f(i, j)}{\delta i}\right)^{2} & \sum_{(i, j) \in W} \frac{\delta f(i, j)}{\delta i} \frac{\delta f(i, j)}{\delta j} \\ \sum_{(i, j) \in W} \frac{\delta f(i, j)}{\delta i} \frac{\delta f(i, j)}{\delta j} & \sum_{(i, j) \in W}\left(\frac{\delta f(i, j)}{\delta j}\right)^{2} \end{array}\right]\left[\begin{array}{l} \Delta i \\ \Delta j \end{array}\right] \end{aligned}$$

基于此，可以计算出其中间的矩阵的特征值$\lambda_{1}, \lambda_{2}$。如果两个特征值都很高，则证明它是一个角（在两个方向上都发生了变化）。如果只有一个特征值高，则证明它是一个边，否则，则证明该区域没有什么变化。基于此，Harris and Stephens提出了以下的角度值衡量策略：

$$C(i, j)=\operatorname{det}(M)-k(\operatorname{trace}(M))^{2}$$

其中k是一个根据经验设定在0.04到0.06之间的常数，然后：

$$M=\left[\begin{array}{cc} \sum_{(i, j) \in W}\left(\frac{\delta f(i, j)}{\delta i}\right)^{2} & \sum_{(i, i) \in W} \frac{\delta f(i, j)}{\delta i} \frac{\delta f(i, j)}{\delta j} \\ \sum_{(i, j) \in W} \frac{\delta f(i, j)}{\delta i} \frac{\delta f(i, j)}{\delta j} & \sum_{(i, j) \in W}\left(\frac{\delta f(i, j)}{\delta j}\right)^{2} \end{array}\right]=\left[\begin{array}{ll} A & B \\ B & C \end{array}\right]$$ $$\begin{aligned} \operatorname{det}(M) &=\lambda_{1} \lambda_{2}=A C+B^{2} \\ \operatorname{trace}(M) &=\lambda_{1}+\lambda_{2}=A+C \end{aligned}$$

实际上，在图像块$W$上进行的加和是加权的，以便给予靠近窗口中心的部分更多的权重。具体来说，它使用了高斯函数来计算权重，例如，一个3x3窗口的权重，如图7.6所示。

Harris角检测器的示例如图7.5和图7.7所示。其计算成本比Moravec要高得多，而且它对噪声也非常敏感，另外，也确实具有一点各向异性的响应（响应随方向而变化）。 但是Harris检测器仍然是最常用的角检测器之一：

1. 其响应非常具有可重复性。
2. 与Moravec检测器相比，它具有更高的检测率（考虑true positives，false positives，true negatives和false negatives的话）。

FAST Corner Detection

FAST（Features from Accelerated Segment Test）检测器与之前的检测器有所不同，因为它并不计算角度值。相反，它会考虑当前像素周围的一个圆上的点（通常半径为3，也就是16个点）。如果圆上有至少9个像素长的连续弧，都比核心（当前点的像素值，或当前点及其周围像素的均值）亮或者暗一个预设的阈值$t$，则当前像素$p$是一个角。选择9是为了排除边，以及实验证明9能给出最优的结果，虽然设置为9会产生一些错误的响应，而在原工作中，将之设置为12，如图7.8所示。

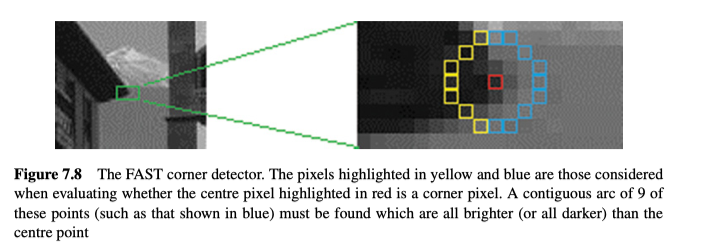
阈值选择值9以排除边缘，并显示出最好的结果，尽管应该清楚的是，在此级别会产生一些错误的响应。实际上，原始工作中建议的值为12。参见图7.8。
由于该方法不计算角度值，所以为了使用非最大值抑制来确保每个角只有一个响应，又另外定义了一个角强度（corner strength），来确定将点$p$分类为一个角时，阈值$t$最大值能为多少。
FAST角检测器，顾名思义，比其他检测器快得多。比如，比Harris的速度要快5-10倍，比SIFT速度要快50倍。示例如图7.9。

SIFT

SIFT（Scale Invariant Feature Transform）是由David Lowe在2004年开发的，其目的是为了给跟踪，识别，全景拼接等，提供可重复且稳定的特征。最厉害的是，其特征不受缩放和旋转影响，受照明和视角的部分不变。与以上的检测器相比，它向前迈出了重要的一步，示例如图7.10所示。

SIFT特征的提取分为多个阶段：

1. 尺度空间极值检测。
2. 准确的关键点定位。
3. 关键点方向分配。
4. 关键点描述子。

此外，也需要具有匹配图像到图像之间的特征的能力，包括识别和删除任何模棱两可的匹配项。

Scale Space Extrema Detection

为了得到不受尺度影响的特征，我们同时从多个尺度来考虑图像，并且在这些图像内定位极值（最大值或最小值）的位置。为此，将图像与多个高斯进行卷积，$L_{\mathrm{n}}(i, j, k, \sigma)=G\left(i, j, k^{n} \sigma\right)^{*} f(i, j)$，其中$n=0,1,2,3, \ldots$，如图7.11所示。

另外，也利用了尺度空间的多个octaves，其中每个octave中的标准偏差是两倍的关系。
为了找到潜在的稳定的关键点位置，我们计算了跨尺度空间的高斯差（DoG，Difference of Gaussian），即$D_{\mathrm{n}}(i, j, k, \sigma)=L_{\mathrm{n}+1}(i, j, k, \sigma)-L_{\mathrm{n}}(i, j, k, \sigma)$，如图7.12所示。

为了找到极值，需要考虑多个DoG图像，并得到那些像素值在当前尺寸和相邻尺寸（更高或更低尺寸）中，都大于（或小于）所有相邻像素点的点，如图7.13所示。

Accurate Keypoint Location

最初，位置和尺度是从中心点获取的，但是这肯定是不准确的，因此，为了更精确地定位关键点，我们使用3D的二次模型对数据进行局部建模，然后就可以找到内插的最大值/最小值。
另外，可以发现，许多确定下来的关键点的鲁棒性不够，因此执行了两次测试，来选择更可靠的关键点。第一个测试考虑了关键点周围区域的局部对比度，它仅仅计算关键点处的二次曲面的曲率，如果曲率低，则表明对比度低，因此应放弃该关键点，如图7.14所示。

第二项测试是检查关键点的位置（例如，它是否只是在边缘上而不是在可区分的特征上）。比如在DoG中，一个定义不明确的峰（即，ridge、脊）将在跨边缘方向上具有较大的主曲率，而在沿边缘方向上具有较小的主曲率。而主曲率，可以根据关键点的位置和尺度，从2x2的Hessian矩阵中计算得到：

$$H=\left[\begin{array}{ll} A & B \\ B & C \end{array}\right]=\left[\begin{array}{ccc} \sum_{(i, j) \in W} \frac{\delta^{2} D_{n}(i, j, k, \sigma)}{\delta i^{2}} & \sum_{(i, j) \in W} \frac{\delta D_{n}(i, j, k, \sigma)}{\delta i} \frac{\delta D_{n}(i, j, k, \sigma)}{\delta j} \\ \sum_{(i, j) \in W} \frac{\delta D_{n}(i, j, k, \sigma)}{\delta i} \frac{\delta D_{n}(i, j, k, \sigma)}{\delta j} & \sum_{(i, j) \in W} \frac{\delta^{2} D_{n}(i, j, k, \sigma)}{\delta j^{2}} \end{array}\right]$$

其中，导数可以通过相邻的样本点的差异来估计，而且对于矩阵来说，trace是对角线的和，determinant是行列式，而trace也等于特征值的和，determinant也等于特征值的乘积。
为了对主曲率进行判断，可以使用与Harris角检测器类似的数学方法，即，仅关注主曲率的比例，从而避免显式的计算特征值。另外，由于矩阵$H$的特征值与$D$的主曲率成正比，所以主曲率的比例可以通过比较特征值来间接得到。令$\lambda_{1}$是较大的特征值，$\lambda_{2}$是较小的特征值。然后，我们可以根据$H$的trace计算特征值之和，并根据行列式计算特征值乘积。

$$\begin{aligned} \operatorname{det}(M) &=\lambda_{1} \lambda_{2}=A C+B^{2} \\ \operatorname{trace}(M) &=\lambda_{1}+\lambda_{2}=A+C \end{aligned}$$

定义$r$为较大特征值与较小特征值之比，即$\lambda_{1}=r \lambda_{2}$。可知，$r$仅取决于特征值的比值，而不取决于它们各自的值。如果将trace的平方除以行列式，可以发现$r$等效于$(r+1)^{2} / r$：

$$\frac{\operatorname{trace}(H)^{2}}{\operatorname{det}(H)}=\frac{\left(\lambda_{1}+\lambda_{2}\right)^{2}}{\lambda_{1} \lambda_{2}}=\frac{\left(r \lambda_{2}+\lambda_{2}\right)^{2}}{r \lambda_{2}^{2}}=\frac{(r+1)^{2}}{r}$$

当两个特征值相等时，其函数值最小，并且随$r$增加而增加，而因为我们已经在第一个测试中舍弃了低曲率的关键点，所以现在只需要考虑曲率的比率即trace的平方除以行列式，低于某个阈值$r\left(T_{r}\right)$即可：

$$\operatorname{Tr}(H)^{2} / \operatorname{Det}(H)<\left(T_{r}+1\right)^{2} / T_{r}$$

不满足该测试的所有特征都将被去除，如图7.14所示，特别在最右的图像中，大量的沿某些竖直边缘的特征被去除了。

Keypoint Orientation Assignment

根据以上内容，我们定义的特征已经不受尺度影响，现在还需要使其不受旋转因素的影响。为此，我们为每个特征分配了一个特定的（主方向）方向。另外，我们根据关键点的尺度来选择具有最接近尺度的高斯平滑图像$L_{\mathrm{n}}$，以便所有计算均以尺度不变的方式执行。之后，对于每个图像样本$L_{\mathrm{n}}(i, j, k, \sigma)$，能计算出该尺度下的梯度大小$\nabla f(i, j)$和方向$\phi(i, j)$：

$$\begin{aligned} \nabla f(i, j) &=\sqrt{\left(L_{\mathrm{n}}(i+1, j, k, \sigma)-L_{\mathrm{n}}(i-1, j, k, \sigma)\right)^{2}+\left(L_{\mathrm{n}}(i, j+1, k, \sigma)-L_{\mathrm{n}}(i, j-1, k, \sigma)\right)^{2}} \\ \phi(i, j) &=\arctan \left(\left(L_{\mathrm{n}}(i+1, j, k, \sigma)-L_{\mathrm{n}}(i-1, j, k, \sigma)\right)^{2},\left(L_{\mathrm{n}}(i, j+1, k, \sigma)-L_{\mathrm{n}}(i, j-1, k, \sigma)\right)^{2}\right) \end{aligned}$$

然后，计算关键点周围的区域内的点的各自方向，来形成具有36个bin，每个bin代表$10^{\circ}$的方向直方图。直方图中添加的每个点均根据其梯度大小，以及高斯权重进行加权，高斯权重根据该点到关键点的距离来定义。
直方图的峰值，意味着关键点周围的梯度的主方向，而最高的峰值则用来定义关键点的方向。值得注意的是，如果还有其他峰的值在最高峰的80％以上，则创建一个新关键点（但方向不同）。通常只有大约15％的关键点被分配了多个方向。

Keypoint Descriptor

提取关键点的最后一步是描述关键点周围的区域，描述子即该区域特征，以便可以将其与其他关键点进行比较。同样，我们使用最接近的尺度的模糊图像，对关键点周围的点进行采样并计算它们的梯度和方向。具体来说，首先按照关键点的方向旋转该区域（这样，所有的方向都是相对关键点的方向计算出来的）。之后，将关键点周围的区域划分为四个子区域，并为分别确定各个子区域的加权直方图（像上面介绍的那样样通过梯度大小和位置加权）。另外，我们将方向映射到对应的bins以及所有相邻的bins中，来减少右量化带来的问题。

Matching Keypoints

为了找到关键点$k$的匹配项，我们必须将关键点的描述子与数据库中的描述子进行比较。另外，可以使用欧几里得距离来匹配，其中最佳匹配可以是距离最小的那个（将描述子作为32维向量进行处理）。这样，所有关键点都将被匹配，但是我们必须将那些在数据库中没有匹配的关键点分离出来。一种方法是在欧几里得距离上使用全局阈值，但这样其实并没有什么用，因为某些描述子会比其他描述子更能区分特征（即某些描述子会有非常不同的结果，而某些描述子可能会非常匹配）。所以，我们选择计算最小欧几里得距离与第二最小的欧几里得距离的比率，并去掉那些比率超过0.8的匹配。从实验上发现，这消除了90％的错误匹配，而且只排除了5％的正确匹配。

Recognition

为了识别对象（对象可能被部分或高度遮挡），我们需要将使用的特征数量最小化。Lowe发现，最少只要三个特征就足够了（而每个图像中通常有2000个或更多特征）。为了找到正确匹配（2000个特征中的匹配）百分比较低的匹配，可以在pose空间中使用霍夫变换（它是四维的-二维用于位置，而另外两维用于尺度和方向） ）。这仅是对完整的六个自由度解的估计值，并不考虑任何非刚性变形。因此，对于位置，应使用最大图像尺寸的四分之一的bin尺寸，比例使用2作为尺度，方向上使用30度。为了避免在将关键点分配到bin时产生边界效应，每个关键点匹配项将被放在每个维度的两个相邻bin中，从而为每个关键点匹配项提供16个条目。
为了找到任何匹配项，我们考虑所有带有至少三个条目的bin，然后在模型和图像之间定义仿射变换。详情见图7.15和图7.16所示。

Other Detectors

其他的特征/角检测器也有很多，比如：

Minimum Eigenvalues

与Harris检测器相似，可以仅使用任意点的最小特征值作为特征强度的度量。这比Harris（在OpenCV中实现）要慢25％，但返回了很多额外的特征（相同的参数设置下）， 见图7.17。

SURF

一种非常常用的特征检测器是SURF（Speeded Up Robust Features），它受到SIFT的启发，旨在更快，更强。随着这些技术的更高效版本的开发，SIFT虽然仍在速度方面略胜一筹。但是大多数研究人员似乎更喜欢使用SURF。因为它能返回更多的额外的特征，虽然SURF比SIFT（在OpenCV中实现）慢大约35％，示例见图7.18和图7.19。

Recognition

上一章中，我们使用一个特征检测器（SIFT），能在比较完一个或多个已知的对象实例的特征和一个可能包含（或可能不包含）该对象的场景的特征之后，去识别场景图像中的对象。这种识别，对于大多数先进的计算机视觉系统至关重要。比如，如果我们想要：

1. 区分不同类型的物体（例如人与汽车，自行车）
2. 辨认特定的个体
3. 自动读取汽车车牌
4. 定位要由机器人操作的特定对物体
5. 识别一本书的页面，特定的绘画或建筑物等，以便我们可以以某种方式来增强现实；
6. 定位眼睛，以便能跟踪它们，进而提供高级的用户交互；
7. 分类物体（例如生产线上的巧克力），以便机器人可以将它们拿起，并放置在正确的位置。

本章继续讨论该主题，并提供了多种不同的识别对象的方法，分别适用于不同情况，但只是计算机视觉中的广泛技术的一小部分。

Template Matching

模板匹配是一种的非常简单的，在图像中搜索子图像的技术，其中子图像表示某些感兴趣的物体。

Applications

模板匹配可用于搜索对象/物体，例如图8.1中所示的窗口。 请注意，虽然这两个模板是从原始图像中获取的，但由于透视投影的原因，图像的顶部较窄，因此各个窗口的外观存在很大差异。

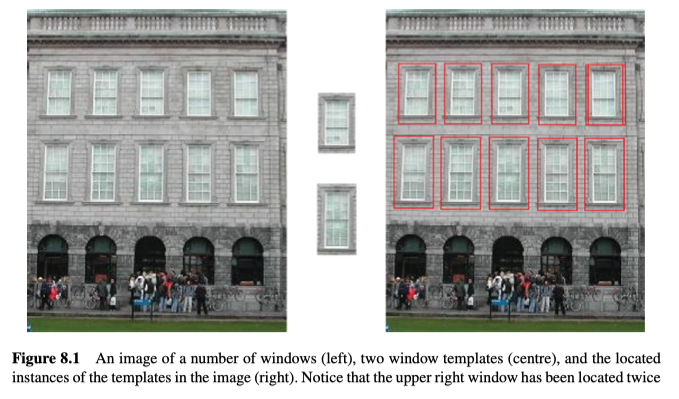
模板匹配可用于某些需要识别的应用，但是在这种情况下，识别是通过直接与图像进行比较来执行的，因此图像之间的差异一定不能太大，否则容易失败。如图8.2所示的例子，识别在以下情况中失败：

• 图像质量差的地方
• 目标图中的字符的字体与模板中的字体不同（例如图8.2中第三个示例中的3）;
• 目标图中的字符未出现在模板中–例如，模板仅包含了数字，而不包含字母。

在工业视觉中，有一种常见的模板匹配的用法，称为golden、黄金模板匹配。在这种用法中，首先提供了一个完美的模板图像（golden template），然后将该模板与所有其他要检查的项目进行比较。将黄金模板与图像对齐后，通常需要计算和分析图像之间的差异，来判断是否存在任何问题。值得注意的是，模板匹配的置信度(confidence level)不足以实现此目标，因为它计算的是全局相似度，而不是识别任何局部的问题。在图8.3的示例中，全局的可信度为99％这么高，但是检查出来的PCB，明显有问题。

模板匹配已被广泛使用（例如，在立体视觉中，我们基于一对双目图像，来确定物体有多远）。我们使用很小的子图像，来寻找一个图像到另一个图像之间的对应关系；在追踪运动对象时，我们通常假设被追踪物体的外观，从帧到帧只会缓慢变化，因此可以在运动物体上使用小模板。

8.1.2 Template Matching Algorithm

模板匹配的输入是一张图像（要进行搜索的场景图像）和一个物体（通常是一个更小的“模板”图像，其中包含我们要寻找的图像），算法如下：

对于图像中每一个可能存在物体对象的位置$(i, j)$：
评估其匹配值并储存子啊匹配空间$M(i, j)$中：
在匹配空间中寻找局部最大值（或最小值）且高于阈值($T$)的地方：

$$\begin{array}{l} (M(i, j)>T) \text { AND }(M(i, j) \geq M(i-1, j-1)) \text { AND }(M(i, j) \geq M(i-1, j)) \text { AND } \\ (M(i, j) \geq M(i-1, j+1)) \text { AND }(M(i, j) \geq M(i, j-1)) \text { AND } \\ \qquad \begin{array}{l} (M(i, j) \geq M(i, j+1)) \text { AND }(M(i, j) \geq M(i+1, j-1)) \text { AND } \\ (M(i, j) \geq M(i+1, j)) \text { AND }(M(i, j) \geq M(i+1, j+1)) \end{array} \end{array}$$

模板和图像的比较结果（即匹配值）存储在匹配空间中。匹配空间小于图像，因为匹配空间的每一个点都是物体在图像中可能存在的位置，而且物体需完全在图像中，如图8.4所示。之后，在匹配空间内搜索局部最大值。通常，局部最大值还必须高于某个阈值。阈值设置得太高会错过某些物体对象，但是若设置得太低会得到一些false positives。

另请注意，“每个可能的位置”可能意味着每个位置（图像空间中的2D搜索）以及对象的每个可能的旋转（会添加另一个维度）以及对象的每个可能的比例（会再次添加另一个维度）。换句话说，如果在搜索时，引入旋转和尺度，将导致四维的匹配空间。这样的自由度的爆炸式增长会使计算复杂性失控，所以通常，会限制这些自由度（例如，将字符识别中的字符的大小和方向归一化处理）。
“匹配标准”（或拟合度）是需要仔细考虑的，因为此标准可能需要处理噪声，部分遮挡，几何失真等问题，因此很难做到精确匹配。

Matching Metrics

为了评估两个图像（一个要在其中搜索的图像$f(i, j)$和模板图像$t(m, n)$）之间的差异，我们可以计算对应像素之间平方差的总和，也可以再对其进行归一化处理（越接近0.0，匹配结果越好）：

$$\begin{aligned} D_{\text {SquareDifferences }}(i, j) &=\sum_{(m, n)}(f(i+m, j+n)-t(m, n))^{2} \\ D_{\text {NormalisedSquareDifferences }}(i, j) &=\frac{\sum_{(m, n)}(f(i+m, j+n)-t(m, n))^{2}}{\sqrt{\sum_{(m, n)} f(i+m, j+n)^{2} \sum_{(m, n)} t(m, n)^{2}}} \end{aligned}$$

我们还可以将欧几里得距离的概念扩展到两个图像之间的距离概念，其中维数是要比较的图像点数。该相似度可以使用互相关性或归一化互相关性来衡量：

$$\begin{aligned} D_{\text {CrossCorrelation }}(i, j) &=\sum_{(m, n)} f(i+m, j+n) \cdot t(m, n) \\ \mathrm{D}_{\text {NormalisedCross Correlation }}(i, j) &=\frac{\sum_{(\mathrm{m}, \mathrm{n})} f(i+m, j+n) \cdot t(m, n)}{\sqrt{\sum_{(\mathrm{m}, \mathrm{n})} f(i+m, j+n)^{2} \sum_{(\mathrm{m}, \mathrm{n})} t(m, n)^{2}}} \end{aligned}$$

这两个指标都是分数越高越好，并且在归一化的互相关性的分数范围从0.0到1.0（完美匹配）。另外，使用归一化互相关性时，即使模板和图像的亮度不同，其返回的结果也不影响，这在匹配时非常有帮助。
另外，当使用平方差之和或归一化平方差之和作为拟合度时，需要搜索最小值，而使用互相关性或归一化互相关性时，需要搜索局部最大值。

Finding Local Maxima or Minima

在处理一阶导数的梯度图像时，我们会沿着某个边缘抑制所有不是局部最大值的梯度点。类似的，在以上的识别技术中，定位局部最大值（或最小值），即non-maxima的最简单形式是将每个值与八个相邻位置的值进行比较，并仅保留那些大于或等于其所有邻居的点。
另外这些最大值点之间的距离不能太近（避免同一匹配产生多个响应），在这种情况下，可以简单地增加与当前点进行比较的邻居的数量。
可以用逻辑测试来执行以上的操作，但也可以先在匹配空间上执行灰度膨胀(dilation)操作，然后直接找到那些值未发生变化且高于某个阈值的点（作为局部最大值）。在这种情况下，膨胀操作的大小限制了最大值之间的最小距离。如图8.5所示。

Control Strategies for Matching

模板匹配的计算成本很高，所以使用它时，需要很仔细的考虑如何有效地执行它。
一种视觉中通用的方法是按图像层次结构（从低分辨率到高分辨率）来处理图像。通过先处理低分辨率图像，进而可以限制高分辨率的处理过程。具体来说，在模板匹配时，可以分析模板的细节程度来确定适当的最低分辨率，然后在以低分辨率计算匹配度后，我们​​可以对其进行阈值处理，来决定在高分辨率中应该识别哪些位置才能得到准确的匹配。
实际上，我们可以进一步考虑这个概念，比如使用较低分辨率下的拟合度来表示较高分辨率下匹配的可能性。然后，我们可以先搜索最高概率的位置，并在找到足够强的匹配项后立即停止（假设我们仅需搜索一个匹配）。虽然采用这种方法意味着有可能会错过有效的匹配项，因为可能在那之前已经停止了。

Chamfer Matching

模板匹配的一个问题是，它要求模板中的物体对象的外观和在搜索图像中的外观几乎一模一样（忽略整体照明情况），外观发生任何失真都可能对匹配分数产生重大影响。
一种基于模板匹配的技术，克服了这个问题-Chamfering Algorithm、倒角匹配。

Chamfering Algorithm

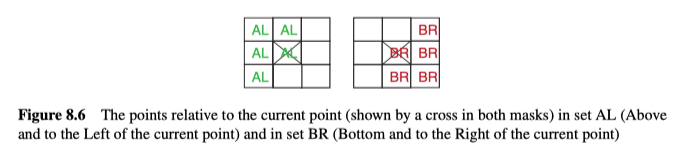
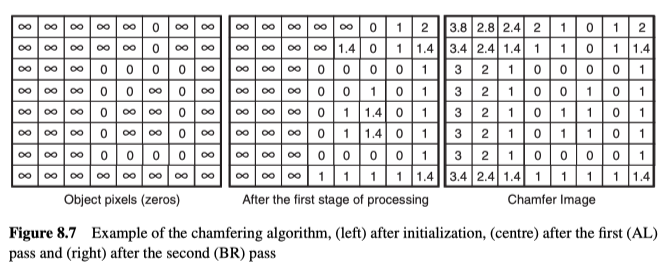
一个像素的倒角值(chamfer value)，是从该像素到最近的物体对象（或边缘）点的距离。通过给每个点搜索最近的对象点，可以为场景中的每个点计算该值。然而，可以想到其计算成本会很高，因此开发出了一个更有效的two-pass操作。第一遍（从上到下，从左到右查看图像中的所有点）考虑当前点$(i, j)$的AL点（如图8.6所示，上方和左侧）。而第二遍考虑（从底部到顶部，从右到左查看图像）考虑了当前点$(i, j)$的BR点（如图8.6所示，下方和右侧）。 实际操作的示例见图8.7所示。

从二元边缘图像$b(i, j)$中计算倒角图像$c(i, j)$的算法如下：

对于所有点：
如果$b(i, j)$是一个边缘点：
设置$c(i, j) = 0$
否侧设置$c(i, j)=\infty$
对于$j$从最小值到最大值：
对于$i$从最小值到最大值：
$c(i, j)=\min _{\mathrm{q} \in \mathrm{AL}}[\operatorname{distance}((i, j), q)+f(q)]$
对于$j$从最大值到最小值：
对于$i$从最大值到最小值：
$c(i, j)=\min _{\mathrm{q} \in \mathrm{BR}}[\operatorname{distance}((i, j), q)+f(q)]$

Chamfer Matching Algorithm

倒角匹配通常用于比较二元的边缘图像（尽管任何二元图像都可以）。倒角匹配中的模板是一个二元模板，其中仅考虑对象物体的像素。之后，将模板在倒角图中的任何可能的位置（与模板匹配相同的方式）进行比较，但是其匹配度是根据，模板中的对象物体像素对应的倒角图中的像素的倒角值，求和计算出来的，如图8.8所示。示例见图8.9。

Statistical Pattern Recognition

如果能从场景的剩余部分中，将单个对象/形状分割出来，之后就能根据从这些对象/形状中提取的特征，对它们进行分类。为此，我们首先需要知道每种已知对象/形状的特征值，之后，我们就能根据未知形状的特征值与已知对象/形状的特征值的相似度，来对其进行分类。

如图8.10所示，以下介绍执行此分类的简单技术，通常称为Statistical Pattern Recognition、统计模式识别。

Probability Review

事件A的概率可以定义为$P(A)=\lim _{n \rightarrow \infty} N(A) / n$，其中$N(A)$是事件$A$在$n$次试验中发生的次数。但需要试验执行很多次，实际概率才会接近理论概率。
如果有两个事件$A$和$B$，而这些事件是独立的，那A和B都发生的概率为：

$$P(A B)=P(A) P(B)$$

而如果它们不独立的话，A发生的概率取决于B是否发生：

$$P(A B)=P(A \mid B) P(B)$$

其中$P(A \mid B) $表示如果B已经发生了，A发生的条件概率。

Probability Density Functions (PDFs)

从统计模式识别的角度来看，我们这样的事件感兴趣：存在某些证据（特征）$x$（例如，测量其圆形度，判断它是硬币的概率）时，未知物体是否属于$W_{\mathrm{i}}$类。在训练时，通过重复的计算$W_{\mathrm{i}}$类的实例的特征，来确定一个特定的特征值($x$)会发生的概率$p\left(x \mid W_{i}\right)$。该概率值$p\left(x \mid W_{i}\right)$实际上就是在某类中发生某值的可能性的Probability Density Functions、概率密度函数。通过计算多个类别的概率密度函数。例如，如果在考虑特征$x$（例如圆形度）对$W_{\mathrm{1}}$类（例如螺母）和$W_{\mathrm{2}}$类（例如垫圈）的影响时，可以为每个类单独的计算概率密度函数，如图8.11所示。

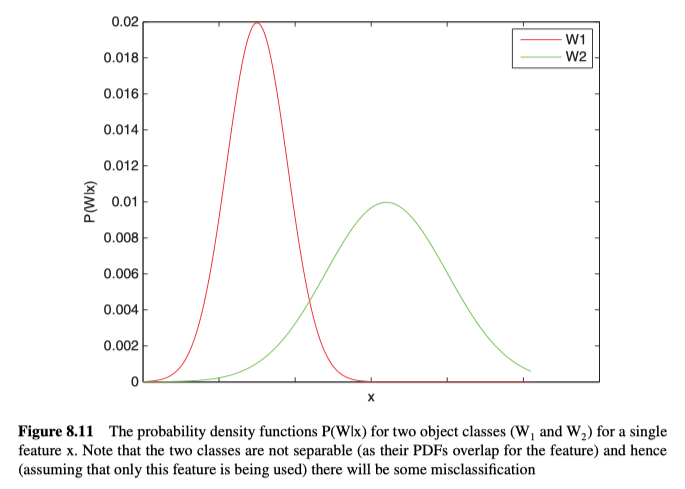
A priori and a posteriori Probabilities

概率$p\left(x \mid W_{i}\right)$是在给定物体对象的类别$W_{\mathrm{i}}$时，特征值/向量$x$会发生的priori、先验概率，但我们通常对后验概率更感兴趣，即如果已经观察到某些特征值/向量$x$，那物体的类别是$W_{\mathrm{i}}$的概率是多少。

Bayes Theorem

我们可以根据先验概率，和各个类别的相对概率（即每个类别的对象发生的频率$p\left(W_{i}\right)$）计算出后验概率。则，对于两个A类和B类，后验概率为：

$$P(B \mid A)=\frac{P(A \mid B) P(B)}{P(A)}$$

其中针对多类别$W_{\mathrm{i}}$时，使用贝叶斯定理：

$$p\left(W_{i} \mid x\right)=\frac{p\left(x \mid W_{i}\right) P\left(W_{i}\right)}{\sum_{j} p\left(x \mid W_{j}\right) P\left(W_{j}\right)}$$

当使用该定理，来对未知对象进行分类时，我们选择具有最大$p\left(W_{i} \mid x\right)$值的类别$W_{\mathrm{i}}$。但是，我们还必须确保$p\left(W_{i} \mid x\right)$的值是合理的（在某个最小阈值之上），以便处理对象不属于任何类别的可能性。

Sample Features

统计模式识别基于与形状/对象关联的某些特征出现的可能性。这些特征通常是根据对象的形状特征计算的，但是同样可以基于对象区域中的颜色或纹理等。 在这里，基于对象形状描述了许多特征。

Area

计算形状的面积可以像计算形状中的像素数一样简单，它已经证明是一项重要的指标，而研究人员可以通过各种不同的算法以及多种不同的表示，来有效地计算面积。比如，根据$n$个多边形顶点$\left(i_{0}, j_{0}\right) \ldots\left(i_{n-1}, j_{n-1}\right)$来计算面积：

$$\text { area }=\frac{1}{2}\left|\sum_{k=0}^{n-1}\left(i_{k} j_{k+1}-i_{k+1} j_{k}\right)\right|$$

该操作很简单，所以也很有趣，最好的解释方法是，比如在一个坐标为(1,1),(1,5),(10,5),(10,1)的正方形上计算面积，这里假设顶点列表是环绕的（即，顶点$n$与顶点$0$相同）。因此面积为$1 / 2 |(5-1)+(5-45)+(5-50)+(10-1)|=1 / 2 |4-40-45+9|=1 / 2 * 72=36$，而这其中，关于原点，每一对都可以被视为两个正方形（其中一个相加，另一个相减）。

Elongatedness

Elongatedness、伸长率（即形状有多长）可以定义为区域面积除以其厚度的平方：

$$\text { elongatedness }=\frac{\text {area}}{(2 d)^{2}}$$

可以通过腐蚀(erosion)来计算其厚度。在所示公式中，$d$是使该区域完全消失所需要腐蚀迭代次数。

Length to Width Ratio for the Minimum Bounding Rectangle

形状的最小边界矩形是将包含形状的最小矩形。要确定此矩形，我们可以考虑所有可能方向上的最小矩形（实际上意味着将其仅旋转一个象限，即90°）并找到最小的矩形。该算法听起来效率很高，但是还有其他更快（但更复杂）的方法来确定矩形，如图8.12所示。

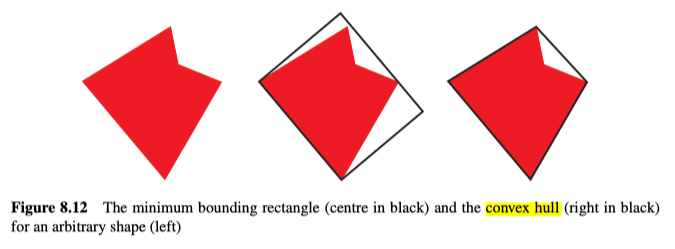
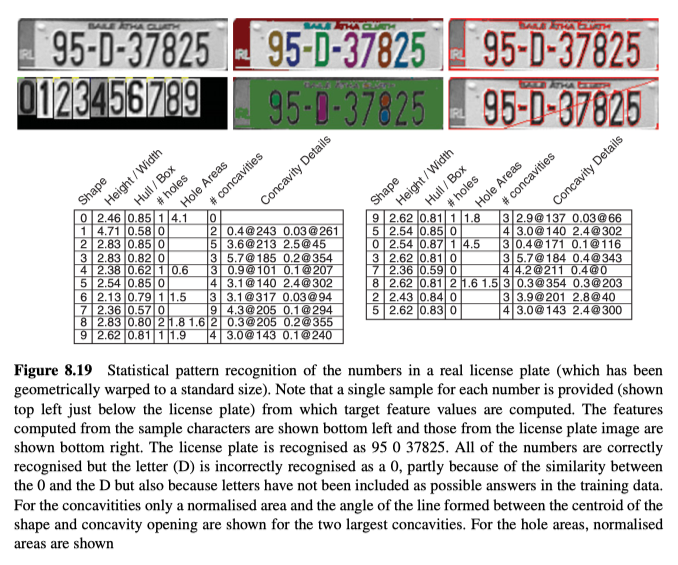
长宽比就是矩形的长度除以矩形的宽度，它能为形状的区分提供有用的度量（例如，在车牌识别中，使用它来区分数字1和所有其他数字，如图8.19所示）。

Convex Hull Area/Minimum Bounding Rectangle Area Ratio

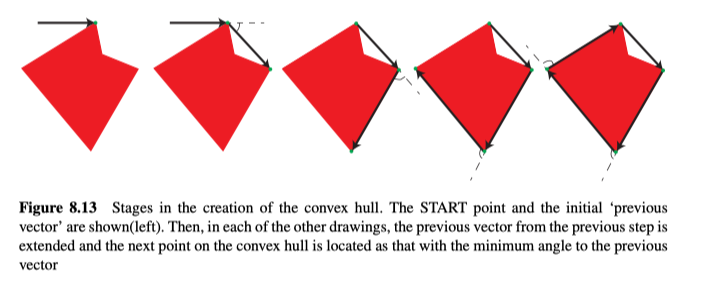
形状的Convex Hull、凸包是包含所有点的最小凸包，如图8.12所示，可以使用以下算法来确定凸包，示例如图8.13所示：

1. 从边界上最左上的点（START）开始，并假定最开始的矢量方向是水平的，从左边指向该点。
2. 搜索形状上的所有其他边界点，并找到与先前的矢量方向的夹角最小的点（NEW）。
3. 切换到新点（NEW），矢量方向从上一个点指向NEW。
4. 如果NEW != START，转到2，否则结束。

然后，可以使用基于多边形顶点列表的面积公式来计算凸包的面积。而Minimum Bounding Rectangle Area、最小边界矩形的面积，就是矩阵的长度乘以矩形的宽度。
该比率只是两个区域的面积商。它也为区分某些形状，提供了一种有用的度量（例如，在车牌识别应用程序中使用它来区分数字1、4和7与所有其他数字，如图8.19所示）。

Concavities and Holes

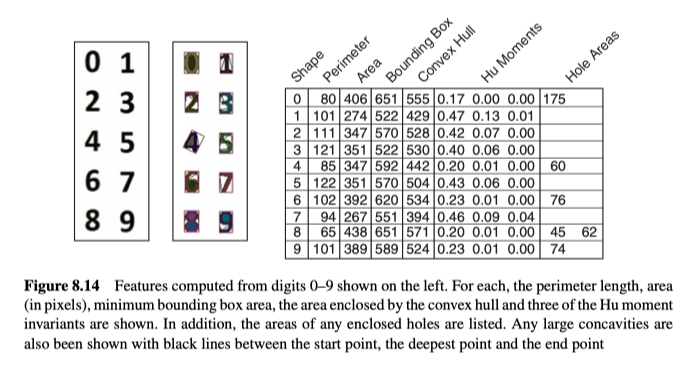
形状中的大凹坑和/或孔的数量以及位置，也能对形状识别有用（例如，它们在车牌识别应用中区分2和5、0和8、6和9之类的数字至关重要，如图8.14和图8.19所示）。

Rectangularity

形状的矩形度是区域的面积与最小矩形边界的面积之比。对于理想的矩形来说，此比率的最大值为1。

Circularity

形状的圆形度是（4 𝜋 面积）除以周长的平方。完整的圆能达到最大值1，周长是通过围绕边界进行描画的，但是在进行此操作时必须注意，要在量化域中进行计算。

Moments and Moment Invariants

Moments可以测量形状的分布，并且可以用作统计模式识别中的特征。

$$M_{x y}=\sum_{i} \sum_{j} i^{x} j^{y} f(i, j)$$

从空间Moments（$M_{\mathrm{xy}}$）中，我们可以计算出不受平移影响的中心Moments（即图像中形状的位置）：

$$\begin{array}{l} \mu_{00}=M_{00} \quad \mu_{01}=0 \quad \mu_{10}=0 \\ \mu_{11}=M_{11}-\frac{M_{10} M_{01}}{M_{00}} \quad \mu_{20}=M_{20}-\frac{M_{10} M_{10}}{M_{00}} \quad \mu_{02}=M_{02}-\frac{M_{01} M_{01}}{M_{00}} \\ \mu_{21}=M_{21}-\frac{2 M_{10} M_{11}}{M_{00}}-\frac{M_{01} M_{20}}{M_{00}}+\frac{2 M_{10} M_{10} M_{01}}{M_{00} M_{00}} \\ \mu_{03}=M_{03}-\frac{3 M_{01} M_{02}}{M_{00}}+\frac{2 M_{01} M_{01} M_{01}}{M_{00} M_{00}} \\ \mu_{12}=M_{21}-\frac{2 M_{01} M_{11}}{M_{00}}-\frac{M_{10} M_{02}}{M_{00}}+\frac{2 M_{10} M_{01} M_{01}}{M_{00} M_{00}} \\ \mu_{30}=M_{30}-\frac{3 M_{10} M_{20}}{M_{00}}+\frac{2 M_{10} M_{10} M_{10}}{M_{00} M_{00}} \end{array}$$

从中心Moments，可以计算出不受尺度影响的Moments：

$$\eta_{x y}=\mu_{x y} / \mu_{00}^{\left(1+^{x+y} / 2\right)}$$

最后，根据以上Moments，我们可以计算出不受旋转（以及位置和尺度）影响的的moment invariants。

$$\begin{array}{l} I_{1}=\eta_{20}+\eta_{02} \\ I_{2}=\left(\eta_{20}-\eta_{02}\right)^{2}+4\left(\eta_{11}\right)^{2} \\ I_{3}=\left(\eta_{30}-3 \eta_{12}\right)^{2}+\left(3 \eta_{21}-\eta_{03}\right)^{2} \\ I_{4}=\left(\eta_{30}+\eta_{12}\right)^{2}+\left(\eta_{21}+\eta_{03}\right)^{2} \\ I_{5}=\left(\eta_{30}-3 \eta_{12}\right)\left(\eta_{30}+\eta_{12}\right)\left(\left(\eta_{30}+\eta_{12}\right)^{2}-3\left(\eta_{21}+\eta_{03}\right)^{2}\right) \\ \quad+\left(3 \eta_{21}-\eta_{03}\right)\left(\eta_{21}+\eta_{03}\right)\left(3\left(\eta_{30}+\eta_{12}\right)^{2}-\left(\eta_{21}+\eta_{03}\right)^{2}\right) \\ I_{6}=\left(\eta_{20}-\eta_{02}\right)\left(\left(\eta_{30}+\eta_{12}\right)^{2}-\left(\eta_{21}+\eta_{03}\right)^{2}\right)+4 \eta_{11}\left(\eta_{30}+\eta_{12}\right)\left(\eta_{21}+\eta_{03}\right) \\ I_{7}=\left(3 \eta_{21}-\eta_{03}\right)\left(\eta_{30}+\eta_{12}\right)\left(\left(\eta_{30}+\eta_{12}\right)^{2}-3\left(\eta_{21}+\eta_{03}\right)^{2}\right) \\ +\left(\eta_{30}-3 \eta_{12}\right)\left(\eta_{21}+\eta_{03}\right)\left(3\left(\eta_{30}+\eta_{12}\right)^{2}-\left(\eta_{21}+\eta_{03}\right)^{2}\right) \end{array}$$

前三个moment invariants可见图8.14中的例子。

Statistical Pattern Recognition Technique

除了从$R$个对象类别$W_{1}, W_{2}, \ldots \quad W_{\mathrm{R}}$中识别出对象类别外，我们还需要考虑，该对象并不是我们以前见过的对象的可能性，但是这个问题经常被忽略。
为了识别对象，我们考虑了从未知实例中提取的信息。该信息采用特征组$\left(x_{1}, x_{2}, \ldots, x_{\mathrm{n}}\right)$的形式，这些特征被称为“输入模式”或特征向量$x$。我们将特征映射到n维特征空间中，如果正确的选择了特征，那么不同的类将映射到特征空间中的特征向量簇，如图8.15所示。理想情况下，这些类应该是可分的，我们应该能够在它们之间建立超曲面。

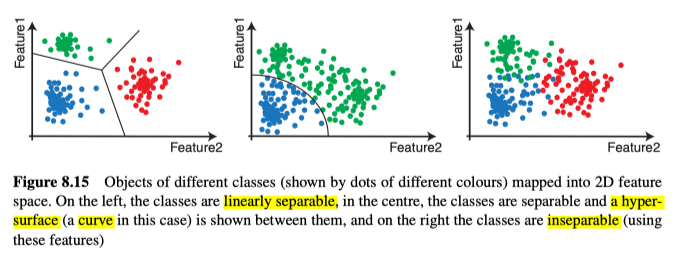
如果超曲面是平面，则这些类别是线性可分离的。虽然对于许多视觉任务来说，这些类不能完全地分离，它会导致一些错误分类。
为了确定哪类对象最能表示特征向量$x$，我们定义了一个decision rule、决策规则$d(x)$，该规则能返回特征$x$对应的类别$W_r$。用于分类的规则有许多，这里介绍其中三个：

• minimum distance classifier, 最小距离分类器
• linear classifier, 线性分类器
• probabilistic classifier，概率分类器

Minimum Distance Classifier

该分类器根据从未知特征向量到多个示例（每个已知的对象类别有一个或多个示例）之间的距离，来确定特征向量所属的类别。而至于示例，通常使用各类的特征向量簇的质心用作示例，以表示该簇中的所有特征向量，如图8.16所示。

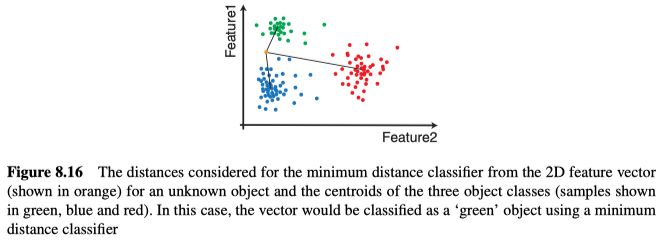
如果一个对象类可以以一种以上的方式出现（例如，一个CD盒，当从上方观察时，它通常看起来几乎是正方形的，但也可能出现在其侧面，在这种情况下，它会显示为细矩形），则可能会导致它出现在特征空间中的多个簇中。另外，如果我们要需要识别出未知类别的对象，则需要为每个或所有类别设置最大距离的阈值。
与更复杂的分类器相比，该方法在计算方面更有优势，因此经常被使用。有关示例，见图8.17所示。

Linear Classifier

要确定特定特征向量最能属于哪种类别的物体，我们可以定义一个决策规则$d(x)$，该规则能返回最佳类别$W_{\mathrm{r}}$，因为对于所有其他类别，都能得到判别函数$g_{\mathrm{r}}(x) \geq g_{\mathrm{s}}(x)$，示例见图8.18所示。另外，为了考虑物体属于未知类别的可能性，$g_{\mathrm{r}}(x)$还需要大于某个最小值。

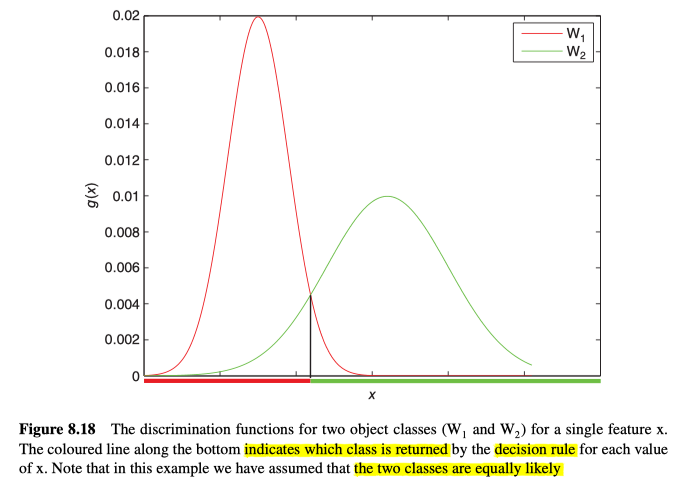
对于$g_{\mathrm{r}}(x)$来说，其最简单的形式可写为一个线性的判别函数：

$$g_{\mathrm{r}}(x)=q_{\mathrm{r}} 0+q_{\mathrm{r} 1} x_{2}+q_{\mathrm{r} 1} x_{2}+q_{\mathrm{r} 3} x_{3}+q_{\mathrm{r} 4} x_{4}+\ldots$$

其中$q$的值是常数。
如果所有类别的分类函数都是线性的，那么这就是一个线性分类器。

Optimal Classifier

错误分类可能会发生，为了使这些错误最小化，应该将最佳分类器设置为概率性的（根据某些损失函数得来），即最佳函数是后验概率，所以每一类别的最佳判别函数可写为以下形式（其中的正则化项$\sum_{j} p\left(x \mid W_{j}\right) P\left(W_{j}\right)$被去除了，因为每一类的正则化项是一样的，去掉不影响比较）：

$$g_{\mathrm{r}}(x)=p\left(x \mid W_{\mathrm{r}}\right) P\left(W_{\mathrm{r}}\right)$$

这就需要对该类（即$p\left(x \mid W_{\mathrm{r}}\right)$）在特征空间上的概率密度函数进行估计，并分别估计该类别的对象发生的相对概率$P\left(W_{\mathrm{r}}\right)$。
因此，平均损失函数（相对于其最佳的分类器）可写为：

$$\begin{aligned} J(q)=& \int_{\mathrm{x}} \sum_{s=1 . R} \lambda\left[d(x, q) \mid W_{\mathrm{s}}\right] p\left(x \mid W_{\mathrm{s}}\right) P\left(W_{\mathrm{s}}\right) d x \\ & \text { where } \lambda\left[W_{\mathrm{r}} \mid W_{s}\right]=\left\{\begin{array}{l} 0 \text { if } r=s \\ 1 \text { otherwise } \end{array}\right. \end{aligned}$$

其中，

• $d(x, q)$是基于模式$x$和每个类别的每个特征的权重，来选择出类别的决策规则。
• $\lambda\left[W_{\mathrm{r}} \mid W_{\mathrm{s}}\right]$表示了将一个本应分类到$W_{\mathrm{s}}$，但是被分类为$W_{\mathrm{s}}$的损失。为了达到最小损失，将任何错误分类的损失值，都设置为固定值1，而对于正确分类，则设置为0。
• $p\left(x \mid W_{\mathrm{s}}\right)$是给出类别$W_{\mathrm{s}}$时，模式$x$的概率。
• $p\left(W_{\mathrm{s}}\right)$是类别$x \mid W_{\mathrm{s}}$出现的概率。

Classifier Training

概率分类器的决策规则的质量基本上取决于概率密度函数的质量以及其所基于的相对类别概率。而这些概率的质量在很大程度上取决于训练集的质量和大小。即该集合必须代表所有可能对象的所有可能的样子，才能让分类器有效的正确识别从未见过的对象。
事先不可能真正定义所需的训练集大小，因此在实验中，通常逐渐增加其大小，直到达到足够的精度为止。
概率可以通过监督的方式来学习，来自动的学习如何将训练集中的样本进行最佳的区分，也可通过无监督的方式学习，即每个样本并未分类，需要在特征空间中聚类来识别潜在类别。但是，在这种情况下，很难自动的选择合适的特征。

Example Using Real Data

最后，我们通过在不受限制的室外环境中拍摄真实图像，来说明该方法的强大，见图8.19所示。

Cascade of Haar Classifiers

本节着眼于两种重要的研究论文中提出的，用于实时的对象/模式识别的高级算法，见图8.20所示。另外，此技术只是众多识别算法中的基础算法。

Features

这些特征是通过对灰度图像内的多个矩形区域（通常为2个或3个）作差得来的，见图8.21所示。

给定一个子图像，将其中一个特征的mask，以某个特定比例，放置在子图像内的某个特定位置，那么特征值就是从白色区域中的像素的归一化总和中减去黑色区域中的归一化总和。其中归一化能调整总和，来使有效面积相同。示例见图8.22所示。

这些特征似乎是合乎逻辑的，即，第一个特征表面脸颊区域比眼睛区域明亮，而第二个似乎表明眼睛之间的空间将比眼睛明亮。

Efficient Calculation – Integral Image

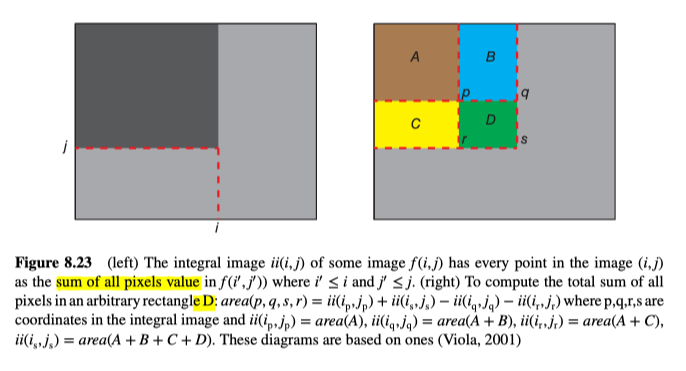
为了使特征的计算更加有效，Viola和Jones提出了Integral image、积分图像的概念。积分图像的大小与从原图中提取出的图像大小相同，并且包含所有坐标较小的像素之和。 由其顶点$(p，q，s，r)$定义任意矩形的面积，可以通过加法和两次减法来计算：

$$i i(i, j)=\sum_{i^{\prime}=0 .. i, {j^{\prime}}=0 .. j}^{\sum} f\left(i^{\prime}, j^{\prime}\right)$$ $$\operatorname{area}(p, q, s, r)=i i\left(i_{\mathrm{p}}, j_{\mathrm{p}}\right)+i i\left(i_{\mathrm{s}}, j_{\mathrm{s}}\right)-i i\left(i_{\mathrm{q}}, j_{\mathrm{q}}\right)-i i\left(i_{\mathrm{r}}, j_{\mathrm{r}}\right)$$

示意图如图8.23所示。这意味着，无论图像的尺度如何，都可以以相同的成本计算特征。这非常重要，因为我们必须在所有可能的比例以及位置上执行计算。

Training

对于典型的子图像，由于特征类型的多样性以及尺寸和位置的变化多样，因此存在数十万种可能的特征。所以必须在训练阶段就确定分类器级联的每个阶段最适合使用哪些特征。为此，必须为系统提供大量的正样本和负样本。

Classifiers

Weak Classifiers

弱分类器可以通过对特定特征进行阈值化处理，以及通过比较来作出接受或拒绝分类来创建。弱分类器可定义为$p_{j}$ feature$_{j}(x)<p_{j} \vartheta_{j}$，其中feature$_{j}(x)$是某个位置$x$处的特征值$j$，$p_{j}$是奇偶校验值，而$\vartheta_{j}$是特征$j$的阈值。必须调整阈值来最大程度地减少误分类的数量（在训练数据上）。

Strong Classifiers – AdaBoost

为了创建强分类器，可以使用增强算法AdaBoost，来将许多弱分类器组合在一起。例如，图8.22所示的两个特征被组合为一个两特征的第一阶段分类器。Viola和Jones还报告说，使用200个特征构建的单个强分类器实现了95％的检测率和0.01％的false positive率。

AdaBoost算法如下：

给定$n$个示例图像$x_{l} .. x_{n}$，其中类别$y_{l} .. y_{n}$，$y_{i}=0,1$分别表示负例子和正例子。

初始化权重

$$w_{1, i}=1 /\left(2 *\left(m^{*}\left(1-y_{i}\right)+l^{*} y_{i}\right)\right)$$

其中$m$和$l$分别是负例子和正例子的数目。
对于$t=1, \ldots, T$

1. 对所有$i$，正则化处理权重： $$w_{t, i}=w_{t, i} /\left(\Sigma_{j = 1 .. n}, w_{t, j}\right)$$
2. 对于每一个特征$j$训练一个弱分类器$h_{\mathrm{j}}(x)$，根据权重计算其误差： $$\varepsilon_{j}=\Sigma_{i} w_{t, i}\left|h_{j}\left(x_{i}\right)-y_{i}\right|$$
3. 选择$\varepsilon_{\mathrm{j}}$最小的分类器$h_{j}(x)$，保存为$c_{\mathrm{t}}(x)$，其中误差为$E_{\mathrm{t}}$。
4. 对所有的$i$更新权重： $$w_{t+1, i}=w_{t, i} \beta_{t}^{(l-e i)}$$ 其中$e_{i}=\left|c_{1}\left(x_{i}\right)-y_{i}\right|$ 以及 $\beta_{t}=E_{1} /\left(1-E_{v}\right)$

而最后的强分类器为：
$
\begin{array}{rl}
h(x)=1& \text{if } \Sigma_{\mathrm{t}=1 . . \mathrm{T}} \alpha_{\mathrm{t}} c_{\mathrm{t}}(x) \geq 1 / 2 \Sigma_{\mathrm{t}=1 . . \mathrm{T}} \alpha_{\mathrm{t}} \\
0& otherwise
\end{array}{}
$
其中$\alpha_{\mathrm{t}}=\log 1 / \beta_{t}$

Classifier Cascade

虽然可以使用单个分类器进行对象识别，但是使用级联的分类器可以提高检测率并减少计算时间。
在级联的每个阶段，都有一个单独的强分类器，可以接受或拒绝所考虑的子图像。如果图像被级联中的分类器拒绝，则不会对该子图像执行进一步的处理。如果分类器接受该分类器，则将其传递到级联中的下一个分类器。以此方式，逐渐将子图像移除考虑，仅留下所要寻找的对象。另外，大多数的负子图像都会被级联中的前两级拒绝，因此这些子图像相对于那些会经过更多级的子图像来说计算量很低，进而减少了计算时间。
另外，级联中的分类器是使用AdaBoost进行训练的，它调整了每个阶段的阈值，以使False Negatives率接近零。

Recognition

Viola和Jones提出的完整的正面人脸检测的级联有38个阶段，一共6000多个特征。在一组4916个正面示例图像和9544个负面示例图像上进行了训练。示例如图8.20和图8.24所示。从各个矩形大小可以看出，图像可以以各种比例进行处理。

Other Recognition Techniques

OpenCV中也支持很多其它的识别技术：

Support Vector Machines (SVM)

支持向量机提供了一种与统计模式识别相似的机制，它试图确定一个最佳的超平面来分离类别。该超平面被放在与“支持向量”（支持向量是各个类中最接近分类边界的具体实例）距离最大的地方。

Histogram of Oriented Gradients (HoG)

Dalal和Triggs提出了定向梯度直方图方法，定位视频以及图片中的站立人的例子，如图8.25所示。它使用线性支持向量机（SVM），基于定向梯度的直方图进行分类。如第6.1.1节所述的方法，计算梯度和方向图像。考虑图像中所有可能的位置，计算多个重叠的方向直方图，其中梯度用作要添加到直方图的权重。

Performance

实际上，在计算机视觉的所有领域（不仅仅是识别），计算时间和性能（成功率和失败率）都非常重要。随着我们频繁的处理大量的数据流，算法重要的是必须要高效且快速。与此同时，由于计算机视觉的许多应用可能至关重要（例如超声/ X射线/ MRI图像中的医学诊断，车辆的自动引导，机器人避障，用于安全系统的面部图像和手印的生物特征分析等），因此也经常需要确保非常高的准确性。
测量视觉操作的计算时间相对简单一点，但是要确定特定视觉算法有多成功则会很困难，它会根据算法所要解决的问题的不同而有所不同。在这里，我们从准确性的角度来考虑性能。
首先要获取一组用于评估任何视觉算法的图像或视频，这些数据集往往非常针对于某个具体问题，所以即使该数据集与算法的要求只有略有不同的形式，都有可能导致用不了。
获得了用于评估的图像数据后，我们面临另外两个问题。要评估任何算法的执行效果，我们需要知道每个图像/视频的最佳答案。这称为真值，通常必须由人类提供/注释。这个真值是非常主观的，因此不同的人类将以不同的方式注释图像/视频。
假设对于要评估的算法，我们现在已经具有令人满意的数据集和真值，那么我们需要可用来量化性能的指标。这些指标根据我们要解决的问题，而有很大不同。

Image and Video Datasets

可用的计算机视觉数据集的范围和数量非常惊人，简单搜索便有上万条信息，此处是其中的一些简单示例：

• http://www.cvpapers.com/datasets.html lists：106个不同的计算机视觉数据集，包括检测汽车，行人，徽标，物体分类，面部识别，跟踪人和车辆，图像分割，前景/背景建模，显着性检测，视觉监控，动作识别，人体姿势确定， 医学影像等。
• http://www.computervisiononline.com/datasets：79个不同的计算机视觉数据集，包括大量不同的数据集，并涵盖了一些不同的领域，例如联合场景检测，3D扫描，图像质量评估，图像配准，光流，指纹识别等。
• http://riemenschneider.hayko.at/vision/dataset/：179个不同的数据集，涵盖了计算机视觉的大多数领域。

Ground Truth

一个非常著名的图像数据集是伯克利分割数据集（http://www.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/segbench/）其中有1000幅图像，由30个人类手动分割，平均每幅图像有12个分割（一半基于彩色图像，另一半基于灰度图像）。标记过程旨在识别出所有人都认为重要的特征。但是，几乎没有两个人对特定图像有着相同的分割意见，这说明了标记真值的困难，如图8.26所示。

尽管人类很难在高层次的分割上达成共识，但更重要的是，在像素级别的分类上也难以达成共识。例如，哪些像素是图像中的moving shadow pixels、移动阴影像素（例如，请考虑图9.3中哪些像素正在移动，并将其与图9.10中的阴影像素进行比较）。

Metrics for Assessing Classification Performance

最终，对于将每个样本归类为正还是负类别的任务来说，我们对分类的成功程度感兴趣。我们想知道我们在避免错误识别的时候，我们的识别任务究竟有多成功。
例如，如果我们试图识别代表可能的安全威胁的机场航站楼中的废弃物体，那么很重要的一点是，我们需要正确地识别大多数（即使不是全部）废弃物体，同时又不会引发太多错误警报。在第一种情况下，丢失的遗弃对象会导致潜在的严重的无法识别的安全威胁。在第二种情况下，如果系统发出过多的虚假警报，则必须调查威胁的安全防护人员将对系统失去信心，并且很可能开始忽略由系统生成的所有警告。评估这两个标准的方法分别称为recall，召回率和precision、精确度，这是计算机视觉中最常遇到的两个性能标准。它们基于四个易于计算的数字：

1. true positives（TP）：已正确识别为所要寻找的类别的样本数（例如，在特定位置存在人脸）。
2. false positives（FP）：被错误地识别为所要寻找类别的样本数（例如，当没有人脸时，在特定位置存在人脸）。
3. true negatives（TN）：已正确标识为不属于所寻求类别的样本数（例如，在特定位置不存在人脸）。
4. false negatives（FN）：被错误地识别为不属于所寻求类别的样本数（例如，当特定位置上存在人脸时，该特定位置不存在人脸）。

测试的样本总数是这四个数字的总和（TotalSamples = TP + FP + TN + FN）。

Recall、召回率是已成功找到的要寻找对象的百分比。

$$\text{Recall}=\frac{T P}{T P+F N}$$

Precision、精度是确认为正确分类中的正确的百分比（即不是错误警报）。

$$\text{Precision}=\frac{T P}{T P+F P}$$

Accuracy、准确度是样本总数中正确的百分比。

$$\text{Accuracy}=\frac{T P+T N}{\text{TotalSamples}}$$

Specificity、特异性，也称为真实阴性率，是正确的阴性分类的百分比。

$$\text{Specificity}=\frac{T N}{F P+T N}$$

$F_{\beta}$度量是精度和召回率的加权度量，可用于对精度和召回率进行不同的强调。

$$F_{\beta}=\left(1+\beta^{2}\right) \cdot \frac{\text { Precision } \cdot \text { Recall }}{\left(\beta^{2} \cdot\right. \text { Precision })+\text { Recall }}$$

$F_{\beta}$度量的三个常用版本。$F_{1}$度量标准对精度和召回率给予了平均重视。$F_{2}$度量对召回率的重视程度比精度高，$F_{0.5}$度量对精度的重视程度高于召回率。
图8.27显示了这些指标的使用示例。

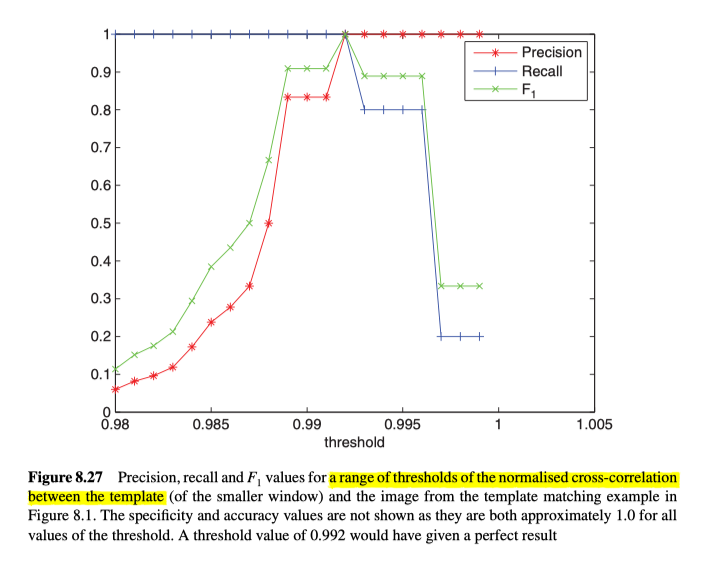
这里描述的评估的一个严重问题是，因为成功（或失败）是在二元的基础上评估的。比如在模板匹配中，真值包括每个匹配窗口的一组准确的位置。如果我们仅将一个像素弄错了位置，其错误将大到好像根本无法识别该窗口一样。因此，很明显，我们需要允许正确匹配的位置略有错误，但仍然被认为是正确的。这可以通过考虑真值中的模板与所定位的模板区域之间的重叠量有多少。但是，我们也要注意，因为我们不想允许单个真值存在多个匹配。

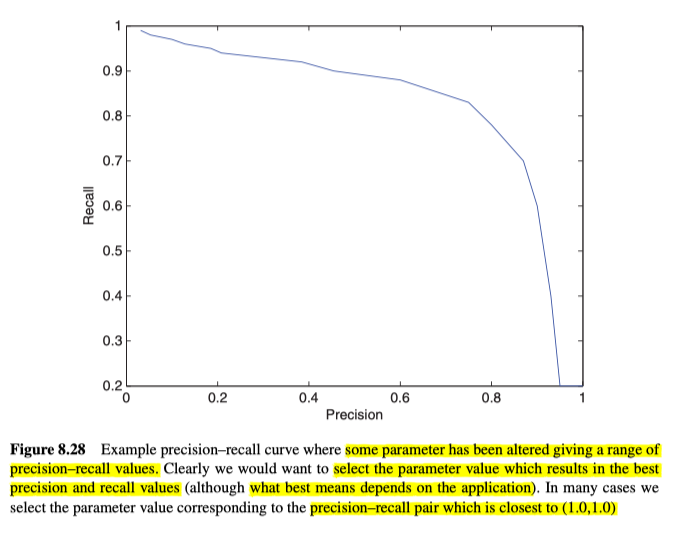
Precision Recall Curves

如果存在可以更修改的参数（例如阈值），则可以为度量确定不同的值集。通常，我们画出一条精度-召回率曲线，该曲线向我们展示了误报与漏报之间的权衡。方便我们选择参数值，来得到适当的精度和召回率，如图8.28所示。

Improving Computation Time

在开发计算机视觉算法时，首先要考虑的是确定问题的可靠解决方案，因为在许多情况下，开发可靠的解决方案非常困难。之后，我们可以再考虑怎样使解决方案更有效。
有许多专门设计的算法可以使得对特定问题的解决方案更加有效。例如，用于中值滤波的Perreault算法（第2.5.4节），Optimal和Otsu阈值算法（第4.2.2和4.2.3节），连通分量算法（第4.5.2节）和倒角算法（第8.2.1节）。
在更通用的方法中，最重要的可能是使用多重分辨率来减少处理量。使用这种方法，我们可以先以低分辨率处理图像，然后进一步确定在更高分辨率中进行研究的位置。此方法已用于图搜索（第6.2.2.3节）和模板匹配（第8.1.5节）中。
其他技术包括在图像处理中使用查找表（第4.1节），在处理视频时使用aging（第9.1.4.5节），使用积分图像（第8.4.1.1节）以及在可能的情况下使用级联，并在级联中的不同级别上有可能拒绝，来避免进一步处理（第8.4.3.3节）。

Video

计算机视觉通常仅使用视频数据流中的静态图像，如工厂的产品检验。但是，如果环境不受限制，其实通过分析视频场景中发生的变化，我们能获得更多有用的信息。

Moving Object Detection

运动检测广泛用来分析包含运动物体（例如汽车和人）的视频序列。场景中这些对象的相对运动可以帮助我们将这些对象从场景的其余部分（背景或其它移动物体）中分割出来。
而大多数的运动检测可用于：

1. 确定图像中是否有任何运动（比如可用于警报）。
2. 检测并定位移动物体。难易程度参差不齐，从仅检测移动物体到跟踪它们，识别它们并预测其未来位置（即它们的预期轨迹）。
3. 提取出3D物体的属性。如果存在一个对象的多个视图（例如，两个摄像机的视图），则可以使用这些视图来确定该对象的3D结构。如果在多个位置看到对象，或者是单个摄像机相对于对象移动，都能得到多个视图。

Object of Interest

我们需要定义感兴趣的对象是什么，这其实并不明显。比如对于监视视频，理想情况下我们希望能知道场景中发生的一切，但实际上如果人或物体只占图像中的很少像素，就无法可靠地定位或跟踪场景背景中的人或物体。所以通常，我们为感兴趣的对象指定最小尺寸（以像素为单位）。
另外，我们假设物体具有最大速度（例如，人只能以某个最大速度运动），而且物体的加速度受到限制（例如，物体不能在一帧内，就从静止变为非常快），而且物体的所有部分都呈现出大致相同的运动（即，它们以大致相同的方式运动，而手臂和腿显然相对于身体的其余部分以周期性的方式运动），并且帧与帧之间会存在对应关系。

Common Problems

此技术遇到的常见问题有：

• 如何应对照明的变化，这种变化可以是渐进的（例如，随着太阳在天空中的位置发生变化）或突然的变化（例如，当太阳落到云层后面或开灯时）。
• 如何确保不会将阴影（可能会导致很大的差异）检测为运动的对象点？一些技术根据亮度，色相和饱和度的变化情况，来解决此问题。另外，如何应对雨水？雨天通常会导致场景变暗，并且使图像变得更加嘈杂。
• 如何考虑有雪的情况？因为这从根本上改变了场景，并在摄像机前添加了大的白色斑点的“噪点”。
• 如何更新背景？物体可能会进入场景并成为背景的一部分（例如，停放时的汽车），或者场景的静态部分也可能会移开（例如，被捡起的手提箱）。
• 如何处理随风飘扬的树木或灌木丛？它们确实是移动对象，但应该忽略它们吗？有一些技术可以为每个像素使用多个值对背景建模，因此，可以允许某个像素在某些时间为绿色（叶子），而在其他时间为蓝色（天空）。
• 相机是移动的还是静态的？它可以平移，倾斜或缩放吗？它有没有任何自动的参数（例如自动对焦）？如果摄像机是完全静态的（没有运动或参数不断变化），分析会简单得多。
• 帧之间的时间间隔是多少？帧之间的时间间隔（以及物体的速度和与相机的距离）对目标物体在图像中移动的最大速度造成了限制。

Difference Images

简单的对图像做减法，就能产生差分图像。那如果计算视频序列$f_{\mathbf{k}}(i, j)$的当前帧与背景图像$b(i, j)$（无运动对象的图像）之间的差，就可以识别场景中，运动物体的点：

• 对于二元图像的输出： $$d(i, j)=\left\{\begin{array}{l} 0 \text { if }\left|f_{\mathrm{k}}(i, j)-b(i, j)\right|<T \\ 1 \text { otherwise } \end{array}\right.$$
• 对于灰度图像： $$d(i, j)=\left|f_{k}(i, j)-b(i, j)\right|$$ 如果要处理彩色图像，则还需要更多考虑，比如是否应该分别处理各个通道，然后选择最大差异（或平均差异），还是应该只处理某些通道（例如色相和亮度），如图9.1所示。

理想情况下，产生的二元差分图像主要都是正确分类的像素，但事实也会有错误的分类像素。我们希望将这些错误分类减至最少，但对于监视的应用来说，我们无法完全消除它们，因为该技术非常依赖于运动对象与静态背景之间的高对比度，但这是无法保证的（因为我们无法约束场景或运动对象的外观）。另外，噪声也会造成影响，可以使用多种技术来将任何小于特定大小的区域去除（例如，二元的open和close），从而抑制噪声。另外，如图9.2所示，阈值$T$太低会出现过多噪声，过高导致很多运动物体无法检测，所以真的不可能做到完美。

Background Models

这种技术的主要部分是对背景模型/图像的获取和维护，相应的有很多算法都可以解决背景问题，如下所示：

Static Background image

最简单方法是直接拍摄场景的静态帧（没有任何移动的物体）。 这是一种很常见的技术，正如许多监视视频都是从完全静态的场景中开始的。但该技术无法处理那些之后添加到场景中，或者从静态场景中删除的物体，也无法应对照明变化甚至是相机或对象位置的微小偏移误差，如图9.3所示。

Frame Difference

解决背景需要更新的问题的一种简单技术是Frame Difference、帧差异技术，它将一帧与前一帧进行比较。移动对象的差异取决于对象移动的数量以及对象的外观，如图9.4所示。但是，对这些差异图像进行分析会非常困难。

Running Average

为了考虑背景的变化，有时会使用运行平均值。运行平均值应该是最后$k$帧的平均值，但这意味着我们必须存储这$k$帧，以便在添加新的帧时可以删除最早的帧。因此，通常使用aging来估算运行平均值下的背景：

$$b_{\mathrm{n}+1}(i, j)=\alpha \cdot f_{\mathrm{n}}(i, j)+(1-\alpha) \cdot b_{\mathrm{n}}(i, j)$$

其中$\alpha$是学习速率。

该运行平均值将不断的更新背景图像，来考虑照明的变化造成的影响。但是，它也将移动的物体考虑到了运行平均值中，图9.5所示，运动物体的模糊会污染背景。

为了减少这种影响，我们可以将帧数（$k$）设置为较高的值，或者将学习率$\alpha$设置为较低的值，但是这样又会让背景适应照明或其他变化的速度非常慢 。另外，如图9.5所示，我们可以分别计算每个通道的运行平均值，来得到彩色图像的运行平均值。
另外，如图9.6所示，在没有移动物体的情况下，背景的噪音将大大降低，但是在有移动物体的情况下，移动物体会产生不良影响。

为了防止前景对象混入背景模型中，其中一种方法是仅更新那些确定为背景点的点。

$$b_{\mathrm{n}+1}(i, j)=\left\{\begin{array}{ll} \alpha \cdot f_{\mathrm{n}}(i, j)+(1-\alpha) \cdot b_{\mathrm{n}}(i, j) & \ldots \text { if } f_{\mathrm{n}}(i, j) \text { is background } \\ b_{\mathrm{n}}(i, j) & \ldots \text { if } f_{\mathrm{n}}(i, j) \text { is foreground } \end{array}\right.$$

如图9.7所示，模糊能减轻了很多，但是，这又带来了新的问题-以哪种方式确定各个点是前景还是背景。如果仅将该点与现有的背景进行比较，则那些后面进入场景并停下来的对象（例如停放的汽车）永远不会成为背景的一部分（因为不会被判定为背景，所以不会渐渐背景，而正因为不会融入背景，所以一直不会被判定为背景），同样的，那些在第一帧就出现的运动物体，由于选择性更新原则，也没有被消除。

针对这个问题，我们可以更改更新方法，来让前景像素也能渐渐混入背景，但是可以设置前景像素的学习率小于那些判定为背景的像素的学习率。例如：

$$b_{\mathrm{n}+1}(i, j)=\left\{\begin{array}{ll} \alpha \cdot f_{\mathrm{n}}(i, j)+(1-\alpha) \cdot b_{\mathrm{n}}(i, j) & \ldots \text { if } f_{\mathrm{n}}(i, j) \text { is background } \\ \alpha / 3 \cdot f_{\mathrm{n}}(i, j)+(1-\alpha / 3) \cdot b_{\mathrm{n}}(i, j) & \ldots \text { if } f_{\mathrm{n}}(i, j) \text { is foreground } \end{array}\right.$$

如图9.8所示，可以发现第一帧出现的运动物体已经被消除了，而后来停着的车，也渐渐平均进入了背景中。

Median Background Image

中位数是值的中间值。通过确定最新$m$帧中对应像素的中值来计算中值背景图像。假设当前帧为$n$，则可以为每个像素计算值的直方图示：

$$h_{\mathrm{n}}(i, j, p)=\sum_{\mathrm{k}=(\mathrm{n}-\mathrm{m}+1) \ldots \mathrm{n}}\left\{\begin{array}{l} 1 \ldots i f\left(f_{\mathrm{k}}(i, j)=p\right) \\ 0 \ldots \text {otherwise } \end{array}\right.$$

然后，再根据这些直方图确定每个像素的中位值。每次处理新帧时，我们都必须删除最旧的值并为每个像素添加新值。这从内存的角度来看，成本很高，因为它要求我们存储$m$帧以及每个像素的直方图。所以我们必须为$m$确定一个适当的值，并限制直方图中的量化，来减少要储存的数据量，尤其是使用彩色图像的时候。
另外，使用aging的形式可以较低成本的更新直方图：

$$\begin{array}{l} h_{\mathrm{n}}(i, j, p)=\sum_{\mathrm{k}=1 . \mathrm{n}}\left\{\begin{array}{l} w_{k} \cdots \text {if } \left.f_{\mathrm{k}}(i, j)=p\right) \\ 0 \ldots \text { otherwise } \end{array}\right. \\ \text { where } w_{1}=1 \text { and } w_{\mathrm{k}}=w_{\mathrm{k}-1}^{*} 1.005 \end{array}$$

这是对实际直方图的近似值，在实践中效果很好，如图9.9所示，其中第一帧的移动物体已经被移除，且停着的车以及融入了背景。

每次处理新帧时，直接从每个帧的每个像素的直方图确定中值在计算上成本会很高。而实际上，直接保存小于或等于当前中值的直方图值之和并在每次更新直方图之后进行少量处理，就可以在成本很低的情况下确认中值的任何变化，如下所示；

对于第一帧：
$\operatorname{total}=1$
对于所有像素$(i, j)$：
$\operatorname{median}(i, j)=f_{1}(i, j)$
$\operatorname{less_than_median}(i, j)=0$

当前帧($n$)：
$\operatorname{total}=\operatorname{total}+w_{\mathrm{n}}$
对于所有的像素$(i, j)$：
如果 $\operatorname{median}(i, j)>f_{\mathrm{n}}(i, j)$
$\operatorname{less_than_median}(i, j)=\operatorname{less_than_median}(i, j)+w_{\mathrm{n}}$
当 $\operatorname{less_than_median}(i, j)+h_{\mathrm{n}}(i, j,\operatorname{median}(i, j))<\operatorname{total} / 2$ 以及 $\operatorname{median}(i, j)<255$ 时="" $\operatorname{less\_than\_median}(i,="" j)="\operatorname{less\_than\_median}(i," j)+h_{\mathrm{n}}(i,="" j,\operatorname{median}(i,="" j))$="" $\operatorname{median}(i,="" j)+1$="" 当=""> \operatorname{total} / 2$ 以及 $\operatorname{median}(i, j) > 0$ 时
$\operatorname{median}(i, j)=\operatorname{median}(i, j)-1$
$\operatorname{less_than_median}(i, j)=\operatorname{less_than_median}(i, j)-h_{\mathrm{n}}(i, j,\operatorname{median}(i, j))$

也可以用同样的方式使用mode（在某些帧上最常使用的值）：

$$b_{\mathrm{n}}(i, j)=p \text { where } h_{\mathrm{n}}(i, j, p) \geq h_{\mathrm{n}}(i, j, q) \text { for all } q \neq p$$

Running Gaussian Average

除了合成图像外，由于多种因素（例如数字化过程本身，照明的轻微变化等），像素的值在帧与帧之间也会有所变化。对于许多现实世界中的噪声，可以使用高斯分布（即具有平均值$\mu$和标准偏差$\sigma$的概率密度函数）来对噪声进行测量和建模。如果该点的值，偏离平均值的值突然是标准偏差的几倍（$k$）以上，则将其定义为前景：

$$\left|f_{n}(i, j)-\mu_{n}(i, j)\right|>k \sigma_{n}(i, j)$$

我们可以使用与运行平均值中用过的相似的方程来更新高斯分布：

$$\begin{array}{l} \mu_{\mathrm{n}+1}(i, j)=\alpha f_{\mathrm{n}}(i, j)+(1-\alpha) \mu_{\mathrm{n}}(i, j) \\ \sigma_{\mathrm{n}+1}^{2}(i, j)=\alpha\left(f_{\mathrm{n}}(i, j)-\mu_{\mathrm{n}}(i, j)\right)^{2}+(1-\alpha) \sigma_{\mathrm{n}}^{2}(i, j) \end{array}$$

同样，如果需要，我们可以使用选择性更新机制，以免前景对象污染高斯分布，以及其他明显的副作用。

Gaussian Mixture Model

到目前为止提到的所有技术都无法处理轻微移动的背景对象（例如，水面上的涟漪，树木在风中移动）。为了解决这个问题，Stauffer和Grimson建议使用混合的高斯分布（通常每个像素3或4个分布）来对背景的每个点建模，如图9.10所示。比如一个像素对应于一棵树上的一片叶子，当叶子随风而规则地移动，露出天空，则使用两个分布，能分别对叶子和天空进行建模。

其基本思想是针对每个点（包括前景和背景值），使用多个高斯分布来拟合历史像素数据。在任何帧（$n$）上，每个高斯分布（$m$）都有一个权重（$\pi_{\mathrm{n}}(i, j, m)$），该权重取决于这个高斯分布在过去的帧中出现的频率。
当考虑一个新的帧时，将每个点$f_{n}(i, j)$与当前对该点建模的高斯分布进行比较，并确定一个最接近的高斯分布（如果有的话）。如果分布与平均值的标准偏差在2.5倍以内，则认为该分布接近。如果没有足够接近的高斯分布，则将初始化一个新的高斯分布以对此点建模。这里的接近，我们定义为它要距离均值在2.5个标准差以内。如果没有足够接近的高斯分布，则初始化一个新的高斯分布来为这一点建模。另外，如果有一个接近的高斯分布，则将该分布更新。对于每个点$f_{\mathrm{n}}(i, j)$，最大的高斯分布（其合至少占到一个设定好的阈值，比如70%）用来表示背景，而一个点分类是背景还是前景，根据它对应的分布到底是前景还是背景。
更新分布：
$\pi_{\mathrm{n}+1}(i, j, m)=\alpha^{} O_{\mathrm{n}}(i, j, m)+(1-\alpha)^{} \pi_{\mathrm{n}}(i, j, m)$
其中，$O_{n}(i, j, m)=1$ 对于最接近的高斯分布，而其他的为0。
$\mu_{\mathrm{n}+1}(i, j, m)=\mu_{\mathrm{n}}(i, j, m)+O_{\mathrm{n}}(i, j, m)^{}\left(\alpha / \pi_{\mathrm{n}+1}(i, j, m)\right)^{}\left(f_{\mathrm{n}}(i, j)-\mu_{\mathrm{n}}(i, j, m)\right)$
$\sigma_{n+1}^{2}(i, j, m)=\sigma_{n+1}^{2}(i, j, m)+O_{n}(i, j, m)^{}\left(\alpha / \pi_{n+1}(i, j, m)\right)^{}\left(\left(f_{n}(i, j)-\mu_{n}(i, j, m)\right)^{2}-\sigma_{n}^{2}(i, j, m)\right)$
其中，$\pi_{\mathrm{n}}(i, j, m)$，$\mu_{\mathrm{n}}(i, j, m)$，$\sigma_{\mathrm{n}}(i, j, m)$分别是第$n$帧在像素$(i, j)$的第$m$个高斯分布的权重，均值和标准差。
通常要为每个像素所考虑的分布数量设置上限，因此，如果必须创建新的分布，则在达到分布数量的限制时，必须丢弃掉校友的最小分布。
请注意，与本章中介绍的所有其他背景模型一样，它是无监督的，因此系统可以学习权重，平均值和标准差，并能够基于在像素上已经观察到的内容对像素进行分类。
尽管已开发出更复杂（且成功）的方法，但以上是最常用的背景建模方法，且常常用作其他背景建模技术的基准。

Shadow Detection

在分析监控视频时，投射的阴影是一个主要问题，因为运动对象的二维形状会因投射的任何阴影而变形。因此，去除这些投射阴影非常重要。 Prati等人开发了一个公式，通过查看背景图像和当前帧之间的hue、色调，以及saturation、饱和度以及本身的值的变化来识别HSV空间中的阴影：

$$S P_{\mathrm{k}}(i, j)=\left\{\begin{array}{l} 1 \ldots i f\left(\alpha<\frac{f_{k}^{V}(i, j)}{B_{k}^{V}(i, j)}<\beta\right) \text { and }\left(\left(f_{k}^{S}(i, j)-B_{k}^{S}(i, j)\right)<\tau_{S}\right) \text { and }\left(\left|f_{k}^{H}(i, j)-B_{k}^{H}(i, j)\right|<\tau_{H}\right) \\ 0 \ldots \text { otherwise } \end{array}\right.$$

当前帧和背景帧中的比值必须在定义的范围内，饱和度必须下降至少$\tau_{\mathrm{S}}$，并且色相的绝对变化必须小于一个小的阈值$\tau_{\mathrm{H}}$，如图9.11所示。

然而，Tattersall发现，在仅考虑值和饱和度变化的情况下，此方法的简化版本效果更好（因为他发现色相的变化有些不可预测）：

$$S P_{\mathrm{k}}(i, j)=\left\{\begin{array}{l} 1 \ldots i f\left(\lambda<\frac{f_{k}^{V}(i, j)}{B_{k}^{V}(i, j)}<1.0\right) \text { and }\left(\left|f_{k}^{S}(i, j)-B_{k}^{S}(i, j)\right|<\tau_{\mathrm{S}}\right) \\ 0 \ldots \text { otherwise } \end{array}\right.$$

$\mu$是通过分析图像数据自动计算出来的，而$\tau_{\mathrm{S}}$被设定到了最大饱和度的12%。

Tracking

跟踪视频中的一个或多个对象是计算机视觉中的一个重要问题，能用于视觉监视，体育视频分析，车辆导航系统，避障等。
视觉跟踪通常并不简单，因为要跟踪的对象会是：

1. 可能正在相对于相机进行复杂的运动。
2. 可能会改变形状（例如，随着手臂，腿部和头部相对于躯干的移动，一个人的外表发生巨大变化）
3. 有时可能被完全或部分遮挡（例如，卡车在行人和摄像机之间通过）；
4. 可能由于光照或天气（例如，打开灯，太阳落在云层下或下雨）而改变外观；
5. 可能会改变外观（例如脱下外套或帽子的人）。

因此，视觉跟踪是一个非常难的问题，而如今已经有很多不同的解决途径。

Exhaustive Search

在最简单的形式中，通过穷举搜索来进行跟踪，其实类似于模板匹配。从要观察的对象的第一帧中提取要跟踪的对象的图像，并使用诸如归一化互相关之类的指标，在以后的帧中的每个可能位置用此模板进行比较。另外，真实世界中的对象可能正在远离或朝向相机移动（并因此在视频中增大或缩小），可能正在旋转（并因此在视频中旋转），或者正在改变它相对于摄像机的视点（因此导致对象的某些部分消失，新的部分出现以及其他部分变形）。因此，至少我们需要考虑四个自由度（两个用于图像位置，一个用于缩放，一个用于图像内的旋转）。对于这些自由度中的任意一个，如果我们对一个对象在两帧之间能对应移动的量作出假设，就可以限制搜索局部最大值的程度。
但是，对于对象可能出现的外观的变化，模板匹配通常根本不起作用，因此开发了其他方法。

Mean Shift

均值偏移是一种迭代的方法，它使用由直方图反投影到图像中确定的概率来定位目标。
要使用均值偏移，我们必须为目标图像提供直方图，以便确定与目标关联的颜色的相对概率。然后可以将这些概率反投影到，我们希望搜索目标的任何图像中。我们还必须提供目标位置的初始估计，并且均值偏移可以有效地搜索，具有与最大求和（和加权）概率大小相同的区域。注意，目标中心的观测值通常比目标边界附近的观测值拥有更大的权重。
均值平移使用爬山算法（一种迭代地移动到本地最大位置的算法）来在给定的概率中迭代地定位最佳目标，因此初始估计很有比较非常接近要搜索的图像中的位置。如图9.12所示。

爬山法（通常称为梯度上升）通过在当前位置迭代的沿最大（向上）梯度的方向，移动来到局部最大值。以这种方式，位置会逐渐更改（一次更改一个像素），直到找到最可能的局部最大值为止。该技术通常在概率（例如，当前位置表示正在寻找的对象的可能性）的空间中使用。但它不能保证定位到全局最大值。

Dense Optical Flow

作为对跟踪特定对象的帮助，我们可以为整个图像计算motion field、运动场。 见图9.13所示。

两个图像之间的2D apparent 运动场称为光流，它显示了图像中每个点的 apparent 运动方向和大小。场景中点的 apparent 运动是由这些点的运动或者相机的运动（或两者）引起的。光流基于亮度恒定性约束，该约束条件指出对象点在短时间内（$\Delta t$）将具有相同的亮度。如果我们考虑在时间$t$拍摄的图像$f_{t}(i, j)$中的点$(i, j)$，假定该点已移动（$\Delta i$，$\Delta j$）：

$$f_{t}(i, j) = f_{t+\Delta t}(i + \Delta i, j + \Delta j)$$

在时间$t$，点$(i, j)$的偏移为（$\Delta i$，$\Delta j$），（$\frac{\Delta i}{\Delta t}$，$\frac{\Delta j}{\Delta t}$）为光流。如果我们为图像中的每个点计算光流矢量，我们将得到一个紧密光流场。（稀疏光流场是仅仅针对图像中的几个点计算出的光场）。一个点的位移$i_{\text{current}}, j_{\text{current}}$可以定义为偏移（$\Delta i$，$\Delta j$），来最小化图像之间的残留误差$\varepsilon$，例如：

$$\varepsilon(\Delta i, \Delta j) = \sum_{i=i_{\text{current}-w}}^{i_\text{current}+w} \sum_{j=j_{\text{current}-w}}^{j_\text{current}+w}f_t(i, j)-f_{t+\Delta t}(i + \Delta i, j + \Delta j)$$

其中，一个小的((2$w$ + 1)×(2$w$ + 1))的围绕当前点的矩形区域被用来评估图像之间的相似性，当然也可以用其他的相似性标准。
我们可以穷举搜索图像$f_{t+\Delta t}(i, j)$来确定最佳匹配，但这样的成本会很高，并且可能会给出错误的结果（例如，如果场景包含多个相似的区域，像棋盘那样）。在许多情况下，图像之间的运动非常小，因此我们可以利用空间的强度梯度来有效地估计偏移量和光流。从一帧到另一帧，图像的外观不会改变很大：

$$f_{t}(i, j)=f_{t+\Delta t}(i + \Delta i, j + \Delta j)$$

如果我们假设帧与帧之间的运动较小，则可以将$f_{t+\Delta t}(i + \Delta i, j + \Delta j)$近似为：

$$f_{t+\Delta t}(i + \Delta i, j + \Delta j)=f_{t}(i, j)+\frac{\partial f}{\partial i} \Delta i + \frac{\partial f}{\partial j} \Delta j + \frac{\partial f}{\partial t} \Delta t$$

实际上，我们通过在时间$t$，给图像在方向和时间上添加运动的估计来逼近新图像。如果将前面的两个方程式结合起来，我们将得到：

$$\frac{\partial f}{\partial i} \Delta i + \frac{\partial f}{\partial j} \Delta j + \frac{\partial f}{\partial t} \Delta t = 0$$

两边除以$\Delta t$得到：

$$\frac{\partial f}{\partial i} \frac{\Delta i}{\Delta t} + \frac{\partial f}{\partial j} \frac{\Delta j}{\Delta t} + \frac{\partial f}{\partial t}$$

即：

$$\begin{bmatrix} \frac{\partial f}{\partial i} \frac{\partial f}{\partial j} \end{bmatrix} \begin{bmatrix} \frac{\Delta i}{\Delta t} \\ \frac{\Delta j}{\Delta t} \end{bmatrix}=-\frac{\partial f}{\partial t}$$

其中值$\frac{\Delta i}{\Delta t}$和$\frac{\Delta j}{\Delta t}$是两个空间方向上的变化率，这些变化率通常被称为光流（即任何点的流矢量）。解决光流方程的一种广泛使用的方法是假设光流在任何点附近的小区域内都是恒定的。因此，我们从方程中对$\frac{\partial f}{\partial i}$，$\frac{\partial f}{\partial j}$，$\frac{\partial f}{\partial t}$值进行了多次观测，并可以使用伪逆来求解$\frac{\Delta i}{\Delta t}$，$\frac{\Delta j}{\Delta t}$。
还有许多其他方法可以计算密集的光流，但OpenCV中最常用的一种方法是Farneback的基于张量的方法。它使用二次多项式来逼近每一帧中每个像素的每个邻域，然后基于具体的多项式在平移下如何变化的知识来估计偏移，如图9.13所示。

Feature Based Optical Flow

计算场景中所有点的光流可能非常困难，甚至不可能。另外，这些计算的成本也可能相当高。因此，我们经常只考虑图像中特征点的光流。正如我们在第7章中看到的那样，特征可以为我们提供独特的模式，这些模式可用于图像之间的匹配，也可以用于帧与帧之间的匹配。因此，如果我们确定了要跟踪的对象，则可以确定哪些特征在中心位置（即不在边界上），然后逐帧匹配这些特征。SIFT和SURF特征特别适合此任务，并且拥有它们自己的匹配特征/关键点的方法。它们不使用光流，而是详尽地比较特征。
基于特征的光流最流行的技术之一是Lucas–Kanade特征跟踪器。特征点是使用特征值技术确定的，其中选择了具有两个高特征值的点，尽管从理论上讲，其他特征检测器（例如Harris）也可以满足要求。
仅在那些特征点处计算光流，如图9.14所示。

Performance

为了评估视频处理任务的性能，例如运动物体检测或跟踪，我们通常需要不同种类的真值和一组与图像中不同的性能评价标准。

Video Datasets (and Formats)

在过去的十年中，在视频处理方面进行了大量研究，并且提供了大量视频和视频数据集，涵盖了广泛的应用，例如视频监视，视频会议，遗留物体检测，事件检测等。这些视频通常没有真值，但那些有真值的，通常采用以下形式之一：

1. 像素标记的mask。这种形式的真值由每个图像（或至少在视频序列中的多个帧中）中的每个像素的标签组成。创建起来非常困难且耗时，但是在评估性能方面能提供最大的准确性。
2. Bounding boxes、边界框。这是创建真值的一种非常容易的形式，因为每个运动对象仅由每个帧中的边界框标识。显然，这些边界框会包含属于其他对象的点，因此在使用它们评估性能时必须格外小心。
3. 带标签的事件。创建真值的最简单形式之一就是事件标签（例如“行李遗弃”，“汽车停下”等）。通常以XML格式。注释的事件差异很大。例如，行李寄存事件，会议室事件，人与人之间的互动事件等。

真值的格式限制了评估表现的方式。 虽然使用基于像素的真值时，能更容易的直接确定精度和回归率的指标，而对于边界框和事件的真值来说，会更难决定如何对其进行处理。

Dice Coefficient

Dice系数通常用于评估跟踪器的逐帧准确性。如果我们将一个被追踪的对象与一个边界框真值进行比较，则可以确定三个区域：一个区域是真值中的边界框，一个区域是被跟踪的对象，另一个区域是两个矩形区域之间的重叠区域（如果有的话），则该系数定义如下：

$$Dice\ coefficient = \frac{2.Area_{Overlap}}{Area_{Object} + Area_{Ground\ Truth}}$$

Dice系数是逐帧计算的。为了捕获跟踪器的“平均”效果，我们计算了序列中的所有Dice系数值的中值（和/或平均值）。

Overlap

跟踪器在给定帧中占据真值边界框的比例，也是评估跟踪器准确性的另一个有用度量：

$$Overlap = \frac{Area_{Overlap}}{Area_{Ground\ Truth}}$$

Lost Tracks/Proportion of Successful Tracks

除了在每个帧上测量给定跟踪器的准确性外，我们还希望知道它在整个跟踪场景中的整体效果。最重要的是，我们必须确定我们何时丢失了对象。此类错误的普遍性是对跟踪器缺乏鲁棒性的一种度量。
我们定义，如果与bounding box、边界框的overlap、重叠部分下落到一个阈值一下，则该追踪器丢失了对象。Nascimento将该值设置为10％，而Kasturi将该阈值设置为20％。两者都很低，但是都非常典型，即使是非常“宽容”，会造成很大的跟踪误差。

Vision Problems

最后一章介绍了一系列的计算机视觉应用问题，可以使用本文介绍的理论（和实践）解决这些问题。

Baby Food

在生产线上，根据婴儿食品罐的制作方法，我们开发一个检查系统，以检查是否已将单个勺子放入其中，如图10.1所示。

Labels on Glue

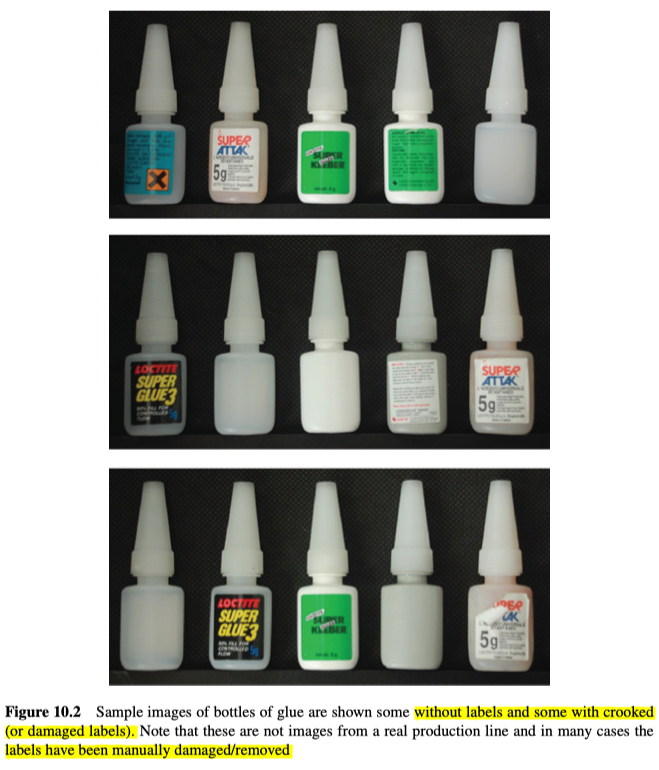
在用于胶水瓶的生产线上，有必要执行许多检查测试，如检测每个胶水瓶是否有标签，是否贴正确，是否有折痕，如图10.2所示：

O-rings

当橡胶O形圈通过检查摄像机之前，需要检测它们的缺陷（缺口和断裂），如图10.3所示。

Staying in Lane

为了协助驾驶员，要求开发一个系统以确保他们驾驶在车道内，并且在他们开始漂移到另一个车道时发出警报。通过安装在汽车仪表板上的向前看的摄像头，获取对应的视频，来自动检测汽车所在车道两侧的线路，如图10.4所示。

Reading Notices

为了便于自动翻译，系统会要求您在图像中找到任何文本并将其提取为一系列字符，如图10.5所示。可能会假设文本占据图像的大部分，并且将以正确的方式排列。

Mailboxes

给定来自监视邮箱的摄像头的视频序列，要求确定每个邮箱中是否有任何邮件，如图10.6所示。为了使处理更容易一些，在每个盒子中都放置了黑白条纹图案。当人们定期放入邮件并从邮箱中取走邮件时，必须能够应对移动人员对相机的遮挡情况（不会产生任何错误的邮件通知）。

Abandoned and Removed Object Detection

要求找到所有废弃的对象和所有被移除的对象，如图10.7和10.8所示。

Surveillance

要求从静态摄像机中找到视频序列中的所有的移动对象并对其进行分类（如人，汽车等），如图10.9所示，它必须能够应对环境影响（例如改变灯光和风的影响等）。

Traffic Lights

要求在摄像机视图中找到所有交通灯，并确定指示灯的颜色（绿色，琥珀色或红色），如图10.10所示。

Real Time Face Tracking

假设Haar分类器的级联速度太慢，那如何在视频中做到（接近）实时的跟踪人脸，如图10.11所示。

Playing Pool

要求分析台球桌上的球的位置以获得可能的设计方式，如图10.12所示。要求仅当桌子上没有球在运动且没有人挡住时，才会去计算球的位置。另外，应报告的是球相对于桌子的位置（而不是图像）。

Open Windows

需要开发一个系统来确定建筑物的图像中，哪些窗户（上悬式）打开了。这能帮助建筑物有效地供暖和通风，如图10.13所示。

Modelling Doors

给定来自监视摄像机的视频，要求您在视图中找到所有门。这可以在训练阶段，用视频或静止图像来完成。这能帮助系统，了解场景中人物的行为，如图10.14所示。

Determining the Time from Analogue Clocks

根据模拟时钟的图像来确定时间，如图10.15所示。

Which Page

需要确定阅读者当前正在查看的，是给定文本中的哪一页（如果有的话），以便可以通过投影仪将增强内容添加到该页面中，如图10.16和图10.17所示。

Nut/Bolt/Washer Classification

要求对那些沿输送线运输的零件（如螺母，螺栓或垫圈或未知物）进行分类，如图10.18所示。

Road Sign Recognition

假设有道路标志的示例（CAD）图像，如图10.19所示，要求开发一个系统，从单个图像（从向前看的汽车的仪表板中获取）中自动识别这些道路标志。这些道路标志会以不同的尺寸出现（随着汽车向它们移动），但应该识别在车辆前面的标志，如图10.20所示。

License Plates

要求识别，用手持摄像机拍摄的车牌上的号码，有两种形式（合成和实数）的数字示例图像，如图10.21、10.22和10.23所示。

Counting Bicycles

要求识别用手持摄像机拍摄的车牌上的号码，数字示例图像有两种形式（合成和实数），如图10.21、图10.22和图10.23所示。

Recognise Paintings

作为增强现实系统的一部分，要求自动的在观察者（摄像机）的视野中确定任何绘画分别是哪一幅画，如图10.25和图10.26所示。